In complex analysis, a removable singularity of a holomorphic function is a point at which the function is undefined, but it is possible to redefine the function at that point in such a way that the resulting function is regular in a neighbourhood of that point.
For instance, the (unnormalized) sinc function
{\displaystyle {\text{sinc}}(z)={\frac {\sin z}{z}}}{\text{sinc}}(z)={\frac {\sin z}{z}}
has a singularity at z = 0. This singularity can be removed by defining {\displaystyle {\text{sinc}}(0):=1,}{\displaystyle {\text{sinc}}(0):=1,} which is the limit of sinc as z tends to 0. The resulting function is holomorphic. In this case the problem was caused by sinc being given an indeterminate form. Taking a power series expansion for {\textstyle {\frac {\sin(z)}{z}}}{\textstyle {\frac {\sin(z)}{z}}} around the singular point shows that
{\displaystyle {\text{sinc}}(z)={\frac {1}{z}}\left(\sum _{k=0}^{\infty }{\frac {(-1){k}z{2k+1}}{(2k+1)!}}\right)=\sum _{k=0}^{\infty }{\frac {(-1){k}z{2k}}{(2k+1)!}}=1-{\frac {z^{2}}{3!}}+{\frac {z^{4}}{5!}}-{\frac {z^{6}}{7!}}+\cdots .}{\text{sinc}}(z)={\frac {1}{z}}\left(\sum _{k=0}^{\infty }{\frac {(-1){k}z{2k+1}}{(2k+1)!}}\right)=\sum _{k=0}^{\infty }{\frac {(-1){k}z{2k}}{(2k+1)!}}=1-{\frac {z^{2}}{3!}}+{\frac {z^{4}}{5!}}-{\frac {z^{6}}{7!}}+\cdots .
Formally, if {\displaystyle U\subset \mathbb {C} }U\subset \mathbb {C} is an open subset of the complex plane {\displaystyle \mathbb {C} }\mathbb {C} , {\displaystyle a\in U}a\in U a point of {\displaystyle U}U, and {\displaystyle f:U\setminus {a}\rightarrow \mathbb {C} }f:U\setminus {a}\rightarrow \mathbb {C} is a holomorphic function, then {\displaystyle a}a is called a removable singularity for {\displaystyle f}f if there exists a holomorphic function {\displaystyle g:U\rightarrow \mathbb {C} }g:U\rightarrow \mathbb {C} which coincides with {\displaystyle f}f on {\displaystyle U\setminus {a}}U\setminus {a}. We say {\displaystyle f}f is holomorphically extendable over {\displaystyle U}U if such a {\displaystyle g}g exists.
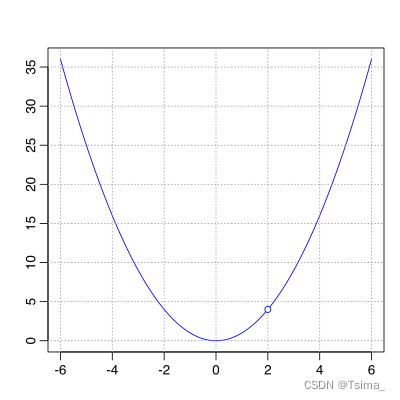
A graph of a parabola with a removable singularity at x = 2
1 Riemann’s theorem
Riemann’s theorem on removable singularities is as follows:
Theorem — Let {\displaystyle D\subset \mathbb {C} }{\displaystyle D\subset \mathbb {C} } be an open subset of the complex plane, {\displaystyle a\in D}a\in D a point of {\displaystyle D}D and {\displaystyle f}f a holomorphic function defined on the set {\displaystyle D\setminus {a}}D\setminus {a}. The following are equivalent:
{\displaystyle f}f is holomorphically extendable over {\displaystyle a}a.
{\displaystyle f}f is continuously extendable over {\displaystyle a}a.
There exists a neighborhood of {\displaystyle a}a on which {\displaystyle f}f is bounded.
{\displaystyle \lim _{z\to a}(z-a)f(z)=0}\lim _{z\to a}(z-a)f(z)=0.
The implications 1 ⇒ 2 ⇒ 3 ⇒ 4 are trivial. To prove 4 ⇒ 1, we first recall that the holomorphy of a function at {\displaystyle a}a is equivalent to it being analytic at {\displaystyle a}a (proof), i.e. having a power series representation. Define
{\displaystyle h(z)={\begin{cases}(z-a)^{2}f(z)&z\neq a,\0&z=a.\end{cases}}}h(z)={\begin{cases}(z-a)^{2}f(z)&z\neq a,\0&z=a.\end{cases}}
Clearly, h is holomorphic on {\displaystyle D\setminus {a}}{\displaystyle D\setminus {a}}, and there exists
{\displaystyle h’(a)=\lim _{z\to a}{\frac {(z-a)^{2}f(z)-0}{z-a}}=\lim _{z\to a}(z-a)f(z)=0}h’(a)=\lim _{z\to a}{\frac {(z-a)^{2}f(z)-0}{z-a}}=\lim _{z\to a}(z-a)f(z)=0
by 4, hence h is holomorphic on D and has a Taylor series about a:
{\displaystyle h(z)=c_{0}+c_{1}(z-a)+c_{2}(z-a){2}+c_{3}(z-a){3}+\cdots ,.}h(z)=c_{0}+c_{1}(z-a)+c_{2}(z-a){2}+c_{3}(z-a){3}+\cdots ,.
We have c0 = h(a) = 0 and c1 = h’(a) = 0; therefore
{\displaystyle h(z)=c_{2}(z-a){2}+c_{3}(z-a){3}+\cdots ,.}h(z)=c_{2}(z-a){2}+c_{3}(z-a){3}+\cdots ,.
Hence, where z ≠ a, we have:
{\displaystyle f(z)={\frac {h(z)}{(z-a)^{2}}}=c_{2}+c_{3}(z-a)+\cdots ,.}f(z)={\frac {h(z)}{(z-a)^{2}}}=c_{2}+c_{3}(z-a)+\cdots ,.
However,
{\displaystyle g(z)=c_{2}+c_{3}(z-a)+\cdots ,.}g(z)=c_{2}+c_{3}(z-a)+\cdots ,.
is holomorphic on D, thus an extension of f.
2 Other kinds of singularities
Unlike functions of a real variable, holomorphic functions are sufficiently rigid that their isolated singularities can be completely classified. A holomorphic function’s singularity is either not really a singularity at all, i.e. a removable singularity, or one of the following two types:
In light of Riemann’s theorem, given a non-removable singularity, one might ask whether there exists a natural number {\displaystyle m}m such that {\displaystyle \lim _{z\rightarrow a}(z-a)^{m+1}f(z)=0}\lim _{z\rightarrow a}(z-a)^{m+1}f(z)=0. If so, {\displaystyle a}a is called a pole of {\displaystyle f}f and the smallest such {\displaystyle m}m is the order of {\displaystyle a}a. So removable singularities are precisely the poles of order 0. A holomorphic function blows up uniformly near its other poles.
If an isolated singularity {\displaystyle a}a of {\displaystyle f}f is neither removable nor a pole, it is called an essential singularity. The Great Picard Theorem shows that such an {\displaystyle f}f maps every punctured open neighborhood {\displaystyle U\setminus {a}}U\setminus {a} to the entire complex plane, with the possible exception of at most one point.
3 See also
Analytic capacity
Removable discontinuity