线性代数 --- 线性代数基本定理下（四个基本子空间他们两两正交，且互为正交补）

2023-11-08

正交子空间

前面我们已经知道了，两个向量的内积为0是勾股定理的另一种表现形式。现在我们来研究一下两个子空间之间的正交。虽然，我很不喜欢一上来就先给个定义，但我这里还是要给，sorry!

现有两个子空间V和W，如果V中的任何一个向量v和W中的任何一个向量w都正交，则子空间V正交于子空间W。

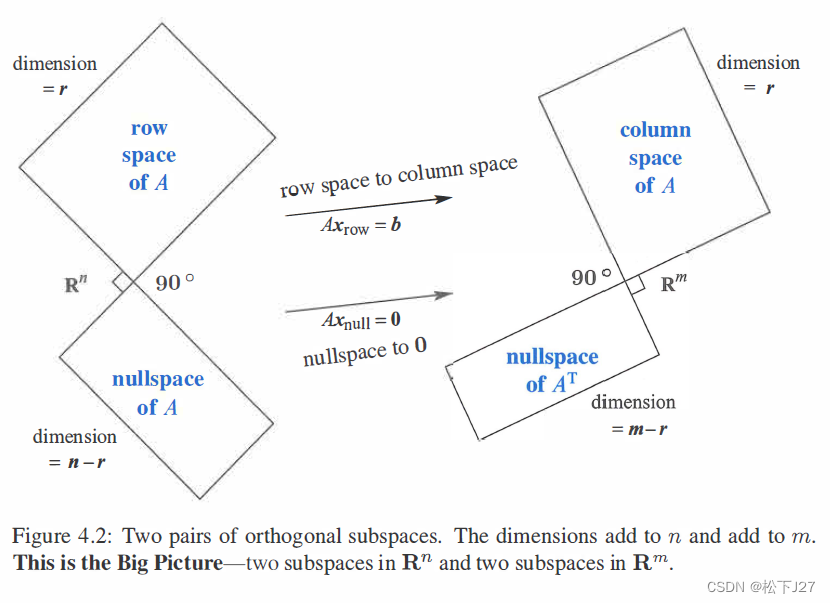
如果说线性代数基本定理的上半部分，告诉了我们A的列空间C(A)与A的行空间C(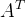 $A^{T}$ )的维数都是r（they are drawn the same size）, 剩下的两个零空间，A的零空间和A的左零空间的维度则分别是n-r和m-r。那么线性代数基本定理的下半部分则告诉我们，这四个基本子空间是两两正交的，且互为正交补。

零空间与行空间正交

对于任何mxn的矩阵A，在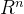 $R^{n}$ 中，A的零空间与行空间正交。记作， $N(A)\perp C(A^{T})$ 。

证明：

首先，我们回到A的零空间的定义，A的零空间是齐次方程组Ax=0，所有的解x的集合。那么，按照零空间的定义，我们在Ax=0的零空间中，随便找一个向量w（他是Ax=0的一个解），他满足Ax=0。现在我们把他展开如下：

$\large Aw=\begin{bmatrix} ... &Row_1 & ...\\ ...& ... &... \\ ... &Row_m & ... \end{bmatrix}\begin{bmatrix} w_1\\ ...\\ w_n \end{bmatrix}= \begin{bmatrix} 0\\ ...\\ 0 \end{bmatrix}$

根据第一行方程，我们得到A的第一行Row1乘以w等于0，根据第二行方程，得到A的第二行Row2乘以w等于0，一直到最后一个方程，A的最后一行Rowm乘以w等于0。按照内积的定义：

$\large x\cdot y=x^{T}y=\begin{bmatrix} x_1 &... &x_n \end{bmatrix}\begin{bmatrix} y_1\\ ...\\ y_n \end{bmatrix}=x_1y_1+...+x_ny_n$

我们有(把n维向量的内积看成是各元素逐一相乘后的累加和):

$\large \begin{matrix} (Row_1ofA)\cdot w=(Col_1ofA^{T})\cdot w=0\\ ...\\ (Row_mofA)\cdot w=(Col_mofA^{T})\cdot w=0 \end{matrix}$

即，Row1正交于w,Row2正交于w......Rowm正交于w。即w正交于A中的每一行，因此，向量w也正交于他们的线性组合，即，A的行空间。(注：一般情况下，我们更喜欢用矩阵转置的列组合来描述A的行空间。即，我们把A中的每行，看成是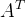 $A^{T}$ 中的每一列，则A中各行的线性组合等价于 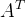$A^{T}$ 中各列的线性组合）如此一来，我们就证明了，向量w正交于A的每一行。

反过来，我们也证明一下A的行空间中的任意一个向量v和零空间中的任意一个向量都正交。设向量x1,x2,....xn是在A的零空间中任意选择的若干个向量。按照零空间的定义，只要向量是A的零空间中的向量，则一定满足方程组Ax1=0,Ax2=0,....Axn=0。又因为行空间中的任意一个向量v，要么是A的某一行，要么是行的线性组合。则，根据前面的方程组，分别有，v乘以v1等于0（即，向量v正交于x1）,向量v正交于x2,.....向量v正交于xn。这说明，A的行空间中的任意一个向量v，正交于A的零空间中的任意向量，因此v正交于A的零空间。

最终得到，A的零空间N(A)正交于A的行空间C(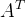 $A^{T}$ )。

例1：

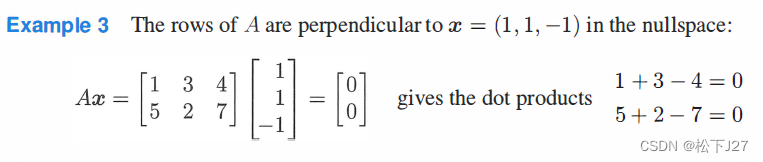
左零空间与列空间正交

对于任何mxn的矩阵A，在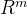 $R^{m}$ 中，A的左零空间与列空间正交。记作， $C(A)\perp N(A^{T})$ 。

证明：

同上，假设w是A的左零空间中的任意一个向量，根据A的左零空间的定义，有：

$\large w^{T}A=\begin{bmatrix} w_1 &... &w_m \end{bmatrix}\begin{bmatrix} ... & ... & ...\\ Col1&... &Coln \\ ...& ...&... \end{bmatrix}=\begin{bmatrix} 0 &... &0 \end{bmatrix}$

然后再根据内积的定义(把n维向量的内积看成是各元素逐一相乘后的累加和)，可知：

$\large \begin{matrix} w_1\cdot Col1=w_1^{T}Col1=0\\ ...\\ w_m\cdot Coln=w_m^{T}Coln=0 \end{matrix}$

由此可见，A的左零空间中的一个任意向量w，正交于A中的每一列，从而他也正交于这些列的每一种线性组合v，而v又是A的列空间中的一个任意向量。因此，我们说，A的左零空间N(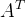 $A^{T}$ )正交于A的列空间C(A)。Q.E.D。

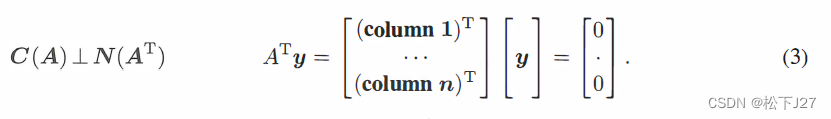
例2：

THE BIG PICTURE（I）

正交补

正交补：

设V是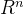 $\large R^{n}$ 的子空间，则所有正交于V的向量所在的空间，叫做V的正交补，记作 $\large V^{\perp }$ 。

根据之前的学习，我们知道了，A的四个基本子空间他们两两正交，即，互为正交子空间。但，事实上，两个正交的子空间V和W，可以互为正交子空间，但不一定是互为正交补。

例如，子空间V是一个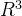 $R^{3}$ 的子空间，是由向量【0，1，0】所张成的一条直线。子空间W也是R3的子空间，是由向量【0，0，1】所张成的一条直线。V和W两个子空间中的任何一个向量都正交，因此得到两个子空间两两正交。但是，两个子空间的维度dim(V)+dim(W)=1+1=2，并不等于3。也就是说两个子空间加在一起并没有充满整个 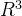$R^{3}$ ，因此，V并不是W的正交补。如下图所示，W+V的组合，只能张成一个二维平面，正好等于二者维度的和2。

实际上，在空间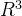 $R^{3}$ 中，子空间W的正交补，应该是一个二维平面（如下图所示），而上图中的V只是一条直线，是W的正交补的一部分。

也就是说，在空间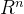 $R^{n}$ 中的两个子空间V和W，如果互为正交补，则两个子空间的维度的和等于n，即两个正交的子空间可以张成整个 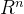$R^{n}$ 空间。即：

两两正交的行空间与零空间互为正交补

考虑上面的这个秩为1的矩阵，已知A的行空间与零空间正交。他的行空间是由向量【1，3】所张成的一条直线。向量【-3，1】'是零空间的基底，他的零空间是常数c和向量【-3，1】张成的一条直线【-3c,c】。因为行空间与零空间互为正交子空间，所以，来自行空间的向量【1，3】，【2，6】，【3，9】和【-3，1】都正交。（或者说，假设向量【x1,x2】是A的零空间的一个任意向量，则一定有向量【1，3】，【2，6】，【3，9】和【x1,x2】都正交）

A的行空间是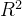 $R^{2}$ 的子空间，维数=rank=1，是一条线。A的零空间也是 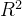$R^{2}$ 的子空间，维数=n-r=1，也是一条直线。我们发现,（零空间的维度=1）+（行空间的维度=1）=（n=2）。这一发现对于其他的所有矩阵也适用，即：

行空间的维度+零空间的维度=矩阵A的列数n

我们发现，A的零空间和行空间的关系，不仅仅是正交，而且，零空间N(A)还包含了所有正交于行空间的向量，反之亦然。

因此，我称A的零空间是行空间的正交补，或者说他们互为正交补。因为，你无法找到一个垂直于A的行空间却不属于A的零空间的向量。

两两正交的列空间与左零空间互为正交补

此外，A的列空间与左零空间正交。向量【1，2，3】是列空间的基底，A的列空间是由它所张成的。向量【1，1，-1】是左零空间的一个解，它与列向量【1，2，3】正交。或者说，对于任何一个左零空间的向量【x1,x2,x3】，一定满足 $x^{T}A=0$ ，因而，一定有向量【x1,x2,x3】和第一列【1，2，3】，第二列【3，6，9】都正交。

A的列空间是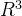 $R^{3}$ 的子空间，维数=rank=1(行秩=列秩)，是由基底【1，2，3】张成的一条直线。A的左零空间也是 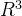$R^{3}$ 的子空间，维数=m-r=2,是由m-r个特解所张成的一个平面。

求解A的左零空间：

$\large A^{T}=\begin{bmatrix} 1 &2 &3 \\ 3& 6 &9 \end{bmatrix}$ $\large U^{T}=\begin{bmatrix} 1 &2 &3 \\ 0& 0 &0 \end{bmatrix}$

共两个自由列，对应两个自由变量x2,x3。

$\large U^{T}x=\begin{bmatrix} 1 &2 &3 \\ 3& 6 &9 \end{bmatrix}\begin{bmatrix} x1\\ x2\\ x3 \end{bmatrix}=0$

现在分别令x2=1,x3=0和x2=0,x3=1分别求解Ux=0,共得到两个特解向量【-2，1，0】和【-3，0，1】，这两个向量都与A的各列正交，且张成了一个二维平面。同样，我们发现，（左零空间的维度=2）+（列空间的维度=1）=（m=3）,推广到其他线性方程组，得到：

列空间的维度+左零空间的维度=矩阵A的行数m

线性代数基本定理下

这样一来，我们就得到了线性代数得基本定理的下半部分，前半部分指出了四个基本子空间的维数，包括行空间的维数等于列空间的维数。但现在我们知道，他们不仅相互垂直，或者说是两两正交，更重要的是他们互为正交补。即：

在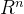 $R^{n}$ 中，零空间与行空间互为正交补。

在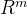 $R^{m}$ 中，列空间与左零空间互为正交补。

再看Ax=b

如此一来，我们又可以从另一个角度去审视线性方程组Ax=b。根据我们之前的理解，只有当b等于A的各列的线性组合时，或者说，只有b属于A的列空间时，Ax=b才有解。（这是Ax=b的一种直观理解）。

而，当我们知道了线性代数基本定理的下半部分以后，我们会说，Ax=b有解，当且仅当b垂直于A的左零空间。（这是Ax=b的一种间接理解）

根据这一定理，有时候，我们不太好判断A的各列是否可以通过线性组合得到b，在这个时候，我们也可以换一种方法，验证一下 $\large y^{T}b$ 是否等于0。

例如：

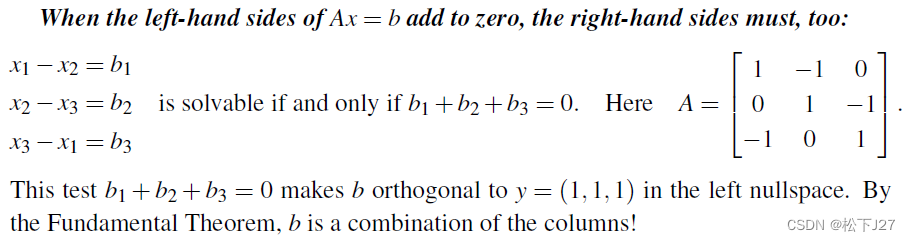
对于上述方程组而言，对于给定的b，我们可以通过判断b是否可以通过A各列的线性组合得到，同时，我们还可以先求出一个左零空间的向量y=(1,1,1)，然后再看判断给定的b是否和y正交。根据向量的内积定理，我们得到b1+b2+b3=0。因此，对于上例中的Ax=b方程组而言，Ax=b是否有界，只需要判断b中所有元素的和是否等于0。这就大大的简化了，我们对方程组是否有解的判断！

THE BIG PICTURE（II）

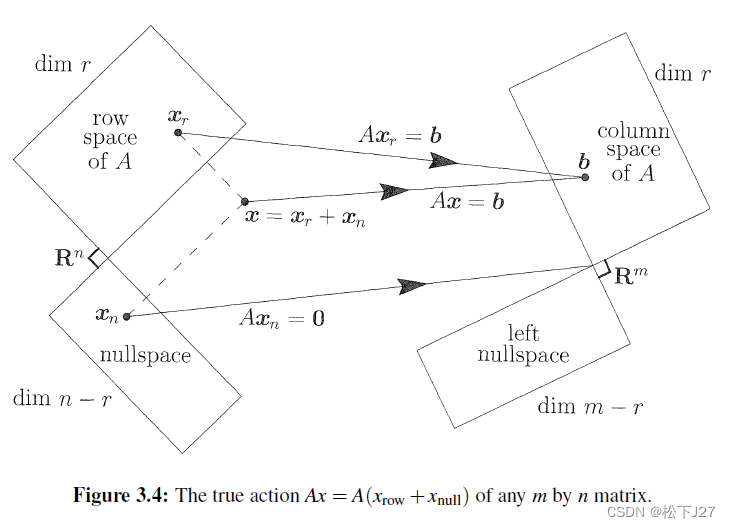
有了线性代数基本定理的下半部分，即他们互为正交补，我们就可以把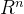 $R^{n}$ 中的任何一个向量，正交分解成属于子空间V的一部分和属于子空间W的另一部分。假设现有3x2的矩阵A，且秩为1，则他的行空间和零空间的维度都分别为1，都是 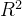$R^{2}$ 的子空间。现在我们把 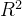$R^{2}$ 这个二维空间看成是充满整个二维坐标的平面，这样一来两个一维的正交子空间就好比是二维坐标系中的x轴与y轴。在二维坐标系中的任何一个向量都可以分解成，沿x轴方向的向量v和沿y轴方向的向量u的和。(如下图所示)

把这个想法推广到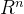 $R^{n}$ 维空间中的任何两个互为正交补的子空间V和W，则，任何一个属于 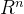$R^{n}$ 的向量x，都可以表示成x=v+u。向量v是x在子空间V上的投影，向量u是x在子空间W上的投影。而这，就是整个线性代数中最重要的一张插图"THE BIG PICTURE（II）"所揭示的内容。

THE BIG PICTURE(II)总结了线性代数的全部基本定理，他是对矩阵A的一种诠释！

1，对于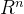 $R^{n}$ 中的一个任意向量x都可以被分解为x= 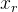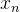$x_{r}$ + $x_{n}$ 这两个分量。

2，矩阵A乘以行空间中的向量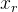 $x_{r}$ ，得到列空间中的向量Ax，即，向量b。即，A 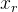$x_{r}$ =Ax=b。

3，矩阵A乘以零空间中的向量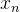 $x_{n}$ ，得到全零向量。即，A 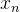$x_{n}$ =0。

综上，如果我们用A乘以分解后的x，得到：

Ax=A( $\large x_{r}$ + $\large x_{n}$ )= A $\large x_{r}$ +A $\large x_{r}$ =b+0=b

（全文完）

作者 --- 松下J27

参考文献(鸣谢)：

1，线性代数及其应用，侯自新，南开大学出版社，1990.

2，Linear Algebra and Its Applications(Fourth Edition) - Gilbert Strang

3，Introduction to Linear Algebra，Fifth Edition - Gilbert Strang

古诗词赏析：

《己亥杂诗》---龚自珍

九州生气恃（shì）风雷，

万马齐喑（yīn）究可哀。

我劝天公重抖擞，

不拘一格降人才。

（配图与本文无关）

本文内容由网友自发贡献，版权归原作者所有，本站不承担相应法律责任。如您发现有涉嫌抄袭侵权的内容，请联系:hwhale#tublm.com(使用前将#替换为@)