组合数学总结

一、组合数学基础

1.1 排列与组合

排列

1. 相异元素不允许重复的排列
   P n r = P ( n , r ) = n ! ( n − r ) ! P_n^r=P(n,r)=\frac{n!}{(n-r)!} Pnr​=P(n,r)=(n−r)!n!​

2. 相异元素允许重复的排列

   从n个不同元素中允许重复的选r个元素的排列，对应的分配模型时将r个有区别的球放入n个不同的盒子，同盒的球不加以区分，每个盒子的球数不加限制且同盒的球不分次序
   R P ( o o , r ) = n r RP(oo,r)=n^r RP(oo,r)=nr

3. 不尽相异元素的排列

   设S={n1·e1, n2·e2, …nt·et}，即元素ei有ni个，且n1+n2+…+nt=n，从S中任取r个元素，求其排列数

   将r个有区别的球放入t个不同的盒子，每个盒子的容量有限，其中第i个盒子最多放ni个球，求分配方案数
   r = = 1 时 ， R P ( n , 1 ) = P t 1 = t r = = n 时 ， R P ( n , n ) = n ! n 1 ! n 2 ! . . . n t ! r==1时，RP(n,1)=P_t^1=t \quad \\ \quad \quad \newline r==n时，RP(n,n)=\frac{n!}{n_1!n_2!...n_t!} r==1时，RP(n,1)=Pt1​=tr==n时，RP(n,n)=n1​!n2​!...nt​!n!​

4. 相异元素不允许重复的圆排列

   C P ( n , n ) = P ( n , n ) n = ( n − 1 ) ! CP(n,n)=\frac{P(n,n)}{n}=(n-1)! CP(n,n)=nP(n,n)​=(n−1)!
   C P ( n , n ) = ( n − 1 ) ! CP(n,n)=(n-1)! CP(n,n)=(n−1)!

例题：

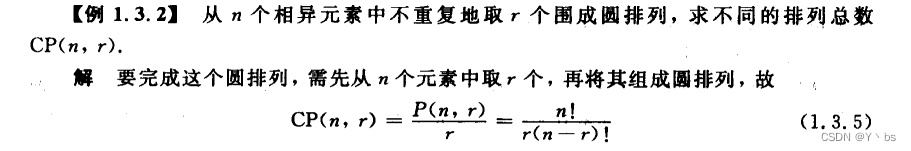
项链排列

隔板思想

组合

1. 相异元素不允许重复的组合
   C n r = = C ( n , r ) = P n r r ! = n ! ( n − r ) ! r ! C_n^r==C(n,r)=\frac{P_n^r}{r!}=\frac{n!}{(n-r)!r!} Cnr​==C(n,r)=r!Pnr​​=(n−r)!r!n!​

2. 相异元素允许重复的组合

   设S={oo · e1, oo · e2, …oo · en}，从S中允许重复的取r个元素构成组合，称r可重组合RC(oo, r)

对应于，将r个无区别的球放入n个不同的盒子，每个盒子的球数不受限制
R C ( o o , r ) = C ( n + r − 1 , r ) = ( n + r − 1 ) ! r ! ( n − 1 ) ! RC(oo,r)=C(n+r-1,r)=\frac{(n+r-1)!}{r!(n-1)!} RC(oo,r)=C(n+r−1,r)=r!(n−1)!(n+r−1)!​

1.2 组合等式及其组合意义

1. 对称关系式
   C ( n , r ) = C ( n , n − r ) C(n,r)=C(n,n-r) C(n,r)=C(n,n−r)

2. 加法公式
   C ( n , r ) = C ( n − 1 , r ) + C ( n − 1 , r − 1 ) C(n,r)=C(n-1,r)+C(n-1,r-1) C(n,r)=C(n−1,r)+C(n−1,r−1)

3. 乘法公式
   C ( n , k ) C ( k , r ) = C ( n , r ) C ( n − r , k − r ) C(n,k)C(k,r)=C(n,r)C(n-r,k-r) C(n,k)C(k,r)=C(n,r)C(n−r,k−r)

1.3 多项式系数

当n是正整数时，Newton二项式定理
( a + b ) n = ∑ r = 0 n ( n r ) a r b n − r 组 合 数 ( n r ) 叫 做 二 项 式 系 数 (a+b)^n=\sum_{r=0}^n\left (\begin{array}{cccc} n \\ r \end{array}\right)a^rb^{n-r} \\\\ \quad \quad \newline 组合数\left (\begin{array}{cccc} n \\ r \end{array}\right)叫做二项式系数 (a+b)n=r=0∑n​(nr​)arbn−r组合数(nr​)叫做二项式系数

定理：
( x 1 + x 2 + . . . + x t ) n 展 开 式 的 项 数 等 于 C ( n + t − 1 , n ) ， 而 这 些 项 的 系 数 之 和 为 t n (x_1+x_2+...+x_t)^n展开式的项数等于C(n+t-1,n)，\\\\ \quad \quad \newline 而这些项的系数之和为t^n \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad (x1​+x2​+...+xt​)n展开式的项数等于C(n+t−1,n)，而这些项的系数之和为tn

例题

二、母函数

2.1 普母函数

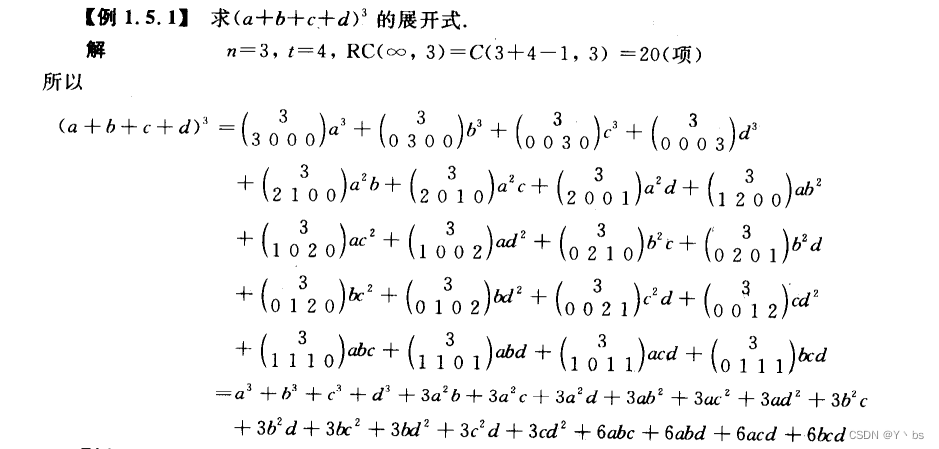
定义：
对 于 数 列 a n ， 称 无 穷 级 数 G ( x ) = ∑ n = 0 o o a n x n 为 该 数 列 的 普 通 型 母 函 数 ， 简 称 普 母 函 数 或 母 函 数 ， 同 时 称 a n 为 G ( x ) 的 生 成 数 列 对于数列{a_n}，称无穷级数G(x)=\sum_{n=0}^{oo}a_nx^n为该数列的普通型母函数，\\ \quad \quad \newline简称普母函数或母函数，同时称{a_n}为G(x)的生成数列 \quad \quad\quad \quad 对于数列an​，称无穷级数G(x)=n=0∑oo​an​xn为该数列的普通型母函数，简称普母函数或母函数，同时称an​为G(x)的生成数列

定理：组合数的母函数
设 S = { n 1 ⋅ e 1 ， n 2 ⋅ e 2 ， . . . ， n m ⋅ e m } ， 且 n 1 + n 2 + . . . n m = n ， 则 S 的 r 可 重 组 合 的 母 函 数 为 G ( x ) = ∏ i = 1 m ( ∑ j = 0 n i x j ) = ∑ r = 0 n a r x r 其 中 ， r 可 重 组 合 数 为 x r 的 系 数 a r ， r = 0 ， 1 , 2... n 设S=\begin{Bmatrix} n_1 · e_1，n_2 · e_2，...，n_m · e_m \end{Bmatrix} ，且n_1+n_2+...n_m=n，\\\\ \quad \quad \newline 则S的r可重组合的母函数为 \quad G(x)=\prod_{i=1}^m(\sum_{j=0}^{n_i}x^j)=\sum_{r=0}^na_rx^r \\\\ \quad \quad \newline 其中，r可重组合数为x^r的系数a_r，r=0，1,2...n \quad \quad \quad \quad 设S={n1​⋅e1​，n2​⋅e2​，...，nm​⋅em​​}，且n1​+n2​+...nm​=n，则S的r可重组合的母函数为G(x)=i=1∏m​(j=0∑ni​​xj)=r=0∑n​ar​xr其中，r可重组合数为xr的系数ar​，r=0，1,2...n

推论
1.
S = { e 1 ， e 2 ， . . . ， e n } ， 则 r 无 重 组 合 的 母 函 数 为 G ( x ) = ( 1 + x ) n 组 合 数 为 x r 的 系 数 C ( n , r ) S=\begin{Bmatrix} e_1， e_2，...，e_n \end{Bmatrix} ，则r无重组合的母函数为 \\ \quad \quad \newline G(x)=(1+x)^n \\ \quad \quad \newline 组合数为x^r的系数C(n,r) S={e1​，e2​，...，en​​}，则r无重组合的母函数为G(x)=(1+x)n组合数为xr的系数C(n,r)
2.
S = { o o ⋅ e 1 ， o o ⋅ e 2 ， . . . ， o o ⋅ e n } ， 则 r 无 限 可 重 组 合 的 母 函 数 为 G ( x ) = ( ∑ j = 0 o o x j ) n = 1 ( 1 − x ) n 组 合 数 为 x r 的 系 数 C ( n + r − 1 , r ) S=\begin{Bmatrix} oo · e_1， oo · e_2，...， oo · e_n \end{Bmatrix} ，则r无限可重组合的母函数为 \\ \quad \quad \newline G(x)=(\sum_{j=0}^{oo}x^j)^n=\frac{1}{(1-x)^n} \\ \quad \quad \newline 组合数为x^r的系数C(n+r-1,r) S={oo⋅e1​，oo⋅e2​，...，oo⋅en​​}，则r无限可重组合的母函数为G(x)=(j=0∑oo​xj)n=(1−x)n1​组合数为xr的系数C(n+r−1,r)

S = { o o ⋅ e 1 ， o o ⋅ e 2 ， . . . ， o o ⋅ e n } ， 每 个 元 素 至 少 取 一 个 ， 则 r 可 重 组 合 ( r ≥ n ) 的 母 函 数 为 G ( x ) = ( ∑ j = 1 o o x j ) n = ( x 1 − x ) n 组 合 数 为 x r 的 系 数 C ( r − 1 , n − 1 ) S=\begin{Bmatrix} oo · e_1， oo · e_2，...， oo · e_n \end{Bmatrix} ，每个元素至少取一个， \\ \quad \quad \newline则r可重组合(r≥n)的母函数为 \quad \quad G(x)=(\sum_{j=1}^{oo}x^j)^n=(\frac{x}{1-x})^n \\ \quad \quad \newline 组合数为x^r的系数C(r-1,n-1) S={oo⋅e1​，oo⋅e2​，...，oo⋅en​​}，每个元素至少取一个，则r可重组合(r≥n)的母函数为G(x)=(j=1∑oo​xj)n=(1−xx​)n组合数为xr的系数C(r−1,n−1)
4.
S = { o o ⋅ e 1 ， o o ⋅ e 2 ， . . . ， o o ⋅ e n } ， 每 个 元 素 出 现 非 负 偶 次 数 ， 则 r 可 重 组 合 的 母 函 数 为 G ( x ) = ( 1 + x 2 + x 4 + . . . + x 2 r + . . . ) = 1 ( 1 − x 2 ) n 组 合 数 为 x r 的 系 数 a r = { 0 ， 当 r 为 奇 数 C ( n + r 2 − 1 ， r 2 ) ， 当 r 为 偶 数 S=\begin{Bmatrix} oo · e_1， oo · e_2，...， oo · e_n \end{Bmatrix} ，每个元素出现非负偶次数， \\ \quad \quad \newline则r可重组合的母函数为 \quad \quad G(x)=(1+x^2+x^4+...+x^{2r}+...)=\frac{1}{(1-x^2)^n} \\ \quad \quad \newline 组合数为x^r的系数 \quad a_r=\left\{ \begin{aligned} 0，当r为奇数 \\ C(n+\frac{r}{2}-1，\frac{r}{2})，当r为偶数 \end{aligned} \right. S={oo⋅e1​，oo⋅e2​，...，oo⋅en​​}，每个元素出现非负偶次数，则r可重组合的母函数为G(x)=(1+x2+x4+...+x2r+...)=(1−x2)n1​组合数为xr的系数ar​=⎩⎨⎧​0，当r为奇数C(n+2r​−1，2r​)，当r为偶数​

例题

二次分配问题

2.2 指母函数

定义
对 于 数 列 { a k } = { a 0 , a 1 , a 2 . . . } G e ( x ) = ∑ n = 0 o o a n x n n ! = a 0 + a 1 x 1 ! + a 2 x 2 2 ! + . . . + a n x n n ! + . . . 称 为 数 列 { a k } 的 指 数 型 母 函 数 ， 简 称 指 母 函 数 ， 而 数 列 { a k } 称 为 指 母 函 数 G e ( x ) 的 生 成 序 列 对于数列\begin{Bmatrix} a_k \end{Bmatrix}=\begin{Bmatrix} a_0,a_1,a_2... \end{Bmatrix} \\ \quad\newline G_e(x)=\sum_{n=0}^{oo}a_n\frac{x^n}{n!}=a_0+a_1\frac{x}{1!}+a_2\frac{x^2}{2!}+...+a_n\frac{x^n}{n!}+... \\ \quad\newline 称为数列\begin{Bmatrix} a_k \end{Bmatrix}的指数型母函数，简称指母函数， \\ \quad\newline 而数列\begin{Bmatrix} a_k \end{Bmatrix}称为指母函数G_e(x)的生成序列 对于数列{ak​​}={a0​,a1​,a2​...​}Ge​(x)=n=0∑oo​an​n!xn​=a0​+a1​1!x​+a2​2!x2​+...+an​n!xn​+...称为数列{ak​​}的指数型母函数，简称指母函数，而数列{ak​​}称为指母函数Ge​(x)的生成序列

定理
设 重 集 S = { n 1 ⋅ e 1 ， n 2 ⋅ e 2 ， . . . ， n m ⋅ e m } ， 且 n 1 + n 2 + . . . + n m = n ， 则 S 的 可 重 排 列 的 指 母 函 数 为 G e ( x ) = ∏ i = 1 m ( ∑ j = 0 n i x j j ! ) = ∑ r = 0 n a r x r r ! 其 中 ， r 可 重 排 列 数 为 x r r ! 的 系 数 a r ， r = 0 , 1 , 2 , . . . n 设重集S=\begin{Bmatrix} n_1 · e_1，n_2 · e_2，...，n_m · e_m \end{Bmatrix} ，\\ \quad\newline 且 n_1+n_2+...+n_m=n，则S的可重排列的指母函数为 \\ \quad\newline G_e(x)=\prod_{i=1}^m(\sum_{j=0}^{n_i}\frac{x^j}{j!})=\sum_{r=0}^na_r\frac{x^r}{r!} \\ \quad\newline 其中，r可重排列数为\frac{x^r}{r!}的系数a_r，r=0,1,2,...n 设重集S={n1​⋅e1​，n2​⋅e2​，...，nm​⋅em​​}，且n1​+n2​+...+nm​=n，则S的可重排列的指母函数为Ge​(x)=i=1∏m​(j=0∑ni​​j!xj​)=r=0∑n​ar​r!xr​其中，r可重排列数为r!xr​的系数ar​，r=0,1,2,...n

例题

二次分配问题

2.3 正整数分拆

定义：将一个正整数n分解成k个正整数之和
{ n = n 1 + n 2 + . . . + n k ， k ≥ 1 n i ≥ 1 ， i = 1 ， 2 ， . . . ， k \left\{ \begin{aligned} n = n_1+n_2+...+n_k， k≥1\\ n_i≥1，i = 1，2，...，k \end{aligned} \right. {n=n1​+n2​+...+nk​，k≥1ni​≥1，i=1，2，...，k​
称该分解是n的一个k分拆，并称n_i为分量。

按照对ni是否要考虑顺序，将分拆分为有序分拆和无序分拆

2.3.1 有序拆分

求n的k有序分拆的个数，相当于求一次不定方程全体正整数解的组数，可对每个分量n_i加以条件限制，例如1 ≤ ni ≤ ri (i = 1, 2, …, k).

定理：对于n的k有序分拆
{ n = n 1 + n 2 + . . . + n k ， k ≥ 1 1 ≤ n i ≤ r i ， i = 1 ， 2 ， . . . ， k \left\{ \begin{aligned} n = n_1+n_2+...+n_k， k≥1\\ 1≤n_i≤r_i，i = 1，2，...，k \end{aligned} \right. {n=n1​+n2​+...+nk​，k≥11≤ni​≤ri​，i=1，2，...，k​

其k有序分拆数列{ qk(n) }的母函数是

∏ i = 1 k ( ∑ j = 1 r i x j ) = ( x + x 2 + . . . + x r 1 ) ( x + x 2 + . . . + x r 2 . . . ) ( x + x 2 + . . . + x r k ) ( x 1 表 示 1 个 1 ， x 2 表 示 2 个 1 ） \prod_{i=1}^k(\sum_{j=1}^{r_i}x^j)=(x+x^2+...+x^{r_1})(x+x^2+...+x^{r_2}...)(x+x^2+...+x^{r_k})\\ \quad \newline (x^1表示1个1，x^2表示2个1） i=1∏k​(j=1∑ri​​xj)=(x+x2+...+xr1​)(x+x2+...+xr2​...)(x+x2+...+xrk​)(x1表示1个1，x2表示2个1）
这个定理等价于，把n个相同的球放入k个不同的盒子里，第i个盒子容量为ri，且使每盒非空

推论：若对n的k有序分拆的各分量ni没有限制，则
其 k 有 序 分 拆 数 数 列 { q k ( n ) } 的 母 函 数 为 ( x 1 − x ) k ， 且 q k ( n ) = C ( n − 1 , k − 1 ) 证 明 ： n = n 1 + n 2 + . . . + n k n − k = ( n 1 − 1 ) + ( n 2 − 1 ) + . . . + ( n k − 1 ) n − k 个 连 续 的 1 中 间 插 入 k − 1 个 0 ， 即 分 为 k 堆 ， C ( n − k + k − 1 , k − 1 ) = C ( n − 1 , k − 1 ) 其k有序分拆数数列\begin{Bmatrix} q_k(n) \end{Bmatrix}的母函数为(\frac{x}{1-x})^k，且 \\\\ \quad \newline q_k(n)=C(n-1,k-1) \\ \quad \newline 证明： n=n_1+n_2+...+n_k \\ \quad \newline n-k=(n_1-1)+(n_2-1)+...+(n_k-1) \\ \quad \newline n-k个连续的1中间插入k-1个0，即分为k堆，C(n-k+k-1,k-1)=C(n-1,k-1) 其k有序分拆数数列{qk​(n)​}的母函数为(1−xx​)k，且qk​(n)=C(n−1,k−1)证明：n=n1​+n2​+...+nk​n−k=(n1​−1)+(n2​−1)+...+(nk​−1)n−k个连续的1中间插入k−1个0，即分为k堆，C(n−k+k−1,k−1)=C(n−1,k−1)

2.3.2 无序拆分

在n的分拆中，不考虑各分量的顺序，就是有序分拆

可以将分拆后的各项数值从大到小加以排序，即有
{ n = n 1 + n 2 + . . . + n k ， k ≥ 1 n 1 ≥ n 2 ≥ n 3 ≥ . . . ≥ n k ≥ 1 满 足 以 上 条 件 的 每 一 组 正 整 数 解 就 代 表 一 个 n 的 k 无 序 分 拆 其 分 拆 数 记 为 p k ( n ) ， n 1 称 为 最 大 分 项 \left\{ \begin{aligned} n = n_1+n_2+...+n_k， k≥1\\ n_1≥n_2≥n_3≥...≥n_k≥1 \end{aligned} \right. \\ \quad \newline 满足以上条件的每一组正整数解就代表一个n的k无序分拆 \\\\ \quad \newline 其分拆数记为p_k(n)，n_1称为最大分项 \quad \quad \quad {n=n1​+n2​+...+nk​，k≥1n1​≥n2​≥n3​≥...≥nk​≥1​满足以上条件的每一组正整数解就代表一个n的k无序分拆其分拆数记为pk​(n)，n1​称为最大分项

将n分拆为k项(每一项的大小不受限制)的分拆数等于将n分拆为最大分项为k(分项个数不限)的分拆数。

把n分拆为最大分项等于k，其分拆数相当于求不定方程
{ 1 x 1 + 2 x 2 + 3 x 3 + . . . + k x k = n x i ≥ 0 , i = 1 , 2 ， . . . k − 1 , x k ≥ 1 \left\{ \begin{aligned} 1x_1+2x_2+3x_3+...+kx_k=n\\ x_i≥0,i=1,2，...k-1,x_k≥1 \end{aligned} \right. {1x1​+2x2​+3x3​+...+kxk​=nxi​≥0,i=1,2，...k−1,xk​≥1​
的整数解的组数。即整数n由1,2，…,k允许重复且k至少出现一次的所有组合数，其母函数为
( 1 + x + x 2 + . . . ) ( 1 + x 2 + ( x 2 ) 2 . . . ) ( 1 + x 3 + ( x 3 ) 2 + . . . ) . . . ( x k + ( x k ) 2 + ( x k ) 3 + . . . ) x k ( 1 − x ) ( 1 − x 2 ) . . . ( 1 − x k ) = ∑ n = k o o p k ( n ) x n (1+x+x^2+...)(1+x^2+(x^2)^2...)(1+x^3+(x^3)^2+...)...(x^k+(x^k)^2+(x^k)^3+...) \\ \quad \newline \frac{x^k}{(1-x)(1-x^2)...(1-x^k)}=\sum_{n=k}^{oo}p_k(n)x^n (1+x+x2+...)(1+x2+(x2)2...)(1+x3+(x3)2+...)...(xk+(xk)2+(xk)3+...)(1−x)(1−x2)...(1−xk)xk​=n=k∑oo​pk​(n)xn
其中展开式中x^n的系数即为n的最大分项等于k的分拆个数

若最大分项小于或等于k，其分拆数相当于求不定方程
{ 1 x 1 + 2 x 2 + 3 x 3 + . . . + k x k = n x i ≥ 0 ， i = 1 ， 2 ， 3 ， 4... k \left\{ \begin{aligned} 1x_1+2x_2+3x_3+...+kx_k=n\\ x_i≥0，i=1，2，3，4...k \end{aligned} \right. {1x1​+2x2​+3x3​+...+kxk​=nxi​≥0，i=1，2，3，4...k​
其分拆数列母函数为
( 1 + x + x 2 + . . . ) ( 1 + x 2 + ( x 2 ) 2 . . . ) ( 1 + x 3 + ( x 3 ) 2 + . . . ) . . . ( 1 + x k + ( x k ) 2 + . . . ) 1 ( 1 − x ) ( 1 − x 2 ) . . . ( 1 − x k ) = ∑ n = 0 o o r k ( n ) x n (1+x+x^2+...)(1+x^2+(x^2)^2...)(1+x^3+(x^3)^2+...)...(1+x^k+(x^k)^2+...) \\ \quad \newline \frac{1}{(1-x)(1-x^2)...(1-x^k)}=\sum_{n=0}^{oo}r_k(n)x^n (1+x+x2+...)(1+x2+(x2)2...)(1+x3+(x3)2+...)...(1+xk+(xk)2+...)(1−x)(1−x2)...(1−xk)1​=n=0∑oo​rk​(n)xn
其中展开式中x^n的系数即为n的最大分项不超过k的分拆个数

三、递推关系

3.1 常系数线性递推关系

k 阶 齐 次 递 推 关 系 ： a n + c 1 a n − 1 + c 2 a n − 2 + . . . + c k a n − k = 0 ， c k ≠ 0 ( 3.1.1 ) k 阶 非 齐 次 递 推 关 系 ： a n + c 1 a n − 1 + c 2 a n − 2 + . . . + c k a n − k = f ( n ) ， c k ≠ 0 ( 3.1.2 ) k阶齐次递推关系： \quad a_n+c_1a_{n-1}+c_2a_{n-2}+...+c_ka_{n-k}=0，c_k≠0 \quad \quad(3.1.1)\\ \\ \\ \quad \quad \newline k阶非齐次递推关系： a_n+c_1a_{n-1}+c_2a_{n-2}+...+c_ka_{n-k}=f(n)，c_k≠0 \quad \quad (3.1.2)\\ k阶齐次递推关系：an​+c1​an−1​+c2​an−2​+...+ck​an−k​=0，ck​​=0(3.1.1)k阶非齐次递推关系：an​+c1​an−1​+c2​an−2​+...+ck​an−k​=f(n)，ck​​=0(3.1.2)

特征根法

1.齐次递推关系

1.1. 特征根为单根
设q1，q2，…，qn是式(3.1.1)的互不相同的特征根，则式(3.1.1)的通解为
a n = A 1 q 1 n + A 2 q 2 n + . . . + A k q k n a_n=A_1q_1^n+A_2q_2^n+...+A_kq_k^n \quad\quad an​=A1​q1n​+A2​q2n​+...+Ak​qkn​

例题

1.2. 重根情况
一般情况下，设q是式(3.2.1)的k重解，则，式(3.1.1)的通解为
a n = ( A 1 + A 2 n + . . . + A k n k − 1 ) q n a_n=(A_1+A_2n+...+A_kn^{k-1})q^n an​=(A1​+A2​n+...+Ak​nk−1)qn

1.3. 复根情况
一般情况，设q是m重复根，自然q’也是m重复根，则通解为
ρ n [ ( A 1 + A 2 n + . . . + A m n m − 1 ) c o s ( n θ ) + ( B 1 + B 2 n + . . . + B m n m − 1 ) s i n ( n θ ) ] ρ^n[(A_1+A_2n+...+A_mn^{m-1})cos(nθ)+(B_1+B_2n+...+B_mn^{m-1})sin(nθ)] ρn[(A1​+A2​n+...+Am​nm−1)cos(nθ)+(B1​+B2​n+...+Bm​nm−1)sin(nθ)]

例题

2.非齐次方程

设a*是式(3.1.2)的一个特解，a’n是式(3.1.1)的通解，则式(3.1.2)的通解为
a n = a n ∗ + a ^ n a_n=a_n^*+\hat{a}_n an​=an∗​+a^n​

2.1. f(n) = b (b为常数)
a n ∗ = A n m a_n^*=An^m an∗​=Anm
其中，m表示1是式(3.1.1)的m重特征根(0≤m≤k），若1不是特征根（即m=0）
a n ∗ = A a_n^*=A an∗​=A

例题

2.2. f(n) = b^n (b为常数)
a n ∗ = A n m n n a_n^*=An^mn^n an∗​=Anmnn
其中m表示b是式(3.1.1)的m重特征根(0≤m≤k）, 若b不是特征根(即m=0)
a n ∗ = A b n a_n^*=Ab^n an∗​=Abn

例题

2.3. f(n) = b^n Pr(n) (其中Pr(n)为关于n的r次多项式，b为常数)
a n ∗ = n m b n Q r ( n ) a_n^*=n^mb^nQ_r(n) an∗​=nmbnQr​(n)
其中Qr(n) 是与Pr(n)同次的多项式，b是式(3.1.1)的m重特征根(0≤m≤k）, 若b不是特征根(即m=0)
a n ∗ = b n Q r ( n ) a_n^*=b^nQ_r(n) an∗​=bnQr​(n)

例题

母函数方法

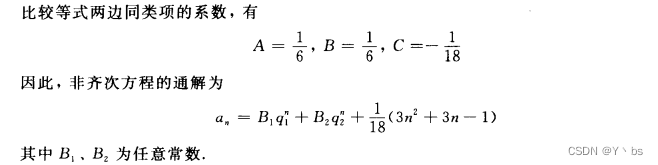
对于一些复杂的递推关系，利用母函数方法求解很有效，当用它求解数列{an}的递推关系时，首先作出{an}的母函数
G ( x ) = ∑ n = 0 o o G(x)=\sum_{n=0}^{oo} G(x)=n=0∑oo​
并以他为媒介，将给定的递推关系转化为关于G(x)的方程，然后解出G(x)，再将G(x)展开成x的幂级数，x^n的系数便是an

例题

Stirling数列

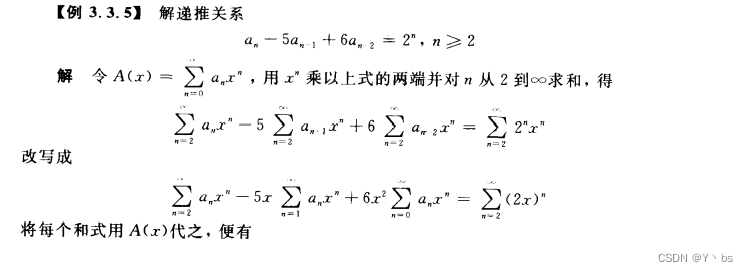
下阶乘函数
[ x ] n = x ( x − 1 ) ( x − 2 ) . . . ( x − ( n − 1 ) ) , [ x ] 0 = 1 [ x ] n = [ x ] n − 1 ∗ ( x − ( n − 1 ) ) ) [x]_n=x(x-1)(x-2)...(x-(n-1)), \quad [x]_0=1 \\ \\ [x]_n=[x]_{n-1}*(x-(n-1))) [x]n​=x(x−1)(x−2)...(x−(n−1)),[x]0​=1[x]n​=[x]n−1​∗(x−(n−1)))

[ x ] n = ∑ k = 0 n S 1 ( n , k ) x k , 其 中 S 1 ( n , k ) 为 第 一 类 S t i r l i n g 数 [ x ] n = ∑ k = 0 n S 2 ( n , k ) x k , 其 中 S 2 ( n , k ) 为 第 二 类 S t i r l i n g 数 [x]_n=\sum_{k=0}^nS_1(n,k)x^k, \quad 其中S_1(n,k)为第一类Stirling数 \\ [x]^n=\sum_{k=0}^nS_2(n,k)x_k, \quad 其中S_2(n,k)为第二类Stirling数 \\ [x]n​=k=0∑n​S1​(n,k)xk,其中S1​(n,k)为第一类Stirling数[x]n=k=0∑n​S2​(n,k)xk​,其中S2​(n,k)为第二类Stirling数

Striling数的组合意义

• 分配问题：将n个有区别的球放入m个相同的盒子，要求各盒不空，则不同的放法为S2(n,m)
• 集合的划分：将含有n个元素的集合恰好分成m个无序非空子集的所有不同划分的数目即S2(n,m)。这种划分也称为集合的m划分

第一类Stirling数的性质

1. S1(n,0)=0
2. S1(n,1)=(n-1)!(-1)^(n-1)
3. S1(n,n)=1
4. S1(n,n-1)=-C(n,2)
5. sgn(S1(n,k))=(-1)^(n+k)
6. S1(n,k)满足递推关系
   S 1 ( n , k ) = S 1 ( n − 1 , k − 1 ) − ( n − 1 ) S 1 ( n − 1 , k ) S_1(n,k)=S_1(n-1,k-1)-(n-1)S_1(n-1,k) S1​(n,k)=S1​(n−1,k−1)−(n−1)S1​(n−1,k)

第二类Stirling数的性质

1. S2(n,0)=0, n>0
2. S2(n,1)=1, n≥1
3. S2(n,n)=1
4. S2(n,n-1)=C(n,2)
5. S2(n,2))=2^(n-1)-1
6. S2(n,k)满足递推关系
   S 2 ( n , k ) = S 2 ( n − 1 , k − 1 ) + k S 2 ( n − 1 , k ) S_2(n,k)=S_2(n-1,k-1)+kS_2(n-1,k) S2​(n,k)=S2​(n−1,k−1)+kS2​(n−1,k)