本篇文章主要介绍快速傅里叶变换(FFT)的优化原理,基-2FFT算法的推导、实现及用FFT实现的线性卷积。
主要参考知乎[精品讲义]—快速傅里叶变换(Fast Fourier Transformation)以及一些数字信号处理的书籍整理而成,参考引用在文末。
FFT是从DFT中优化而来的,首先,给出对一个长度为N的离散信号的DFT表达式:
X
(
k
)
=
∑
n
=
0
N
−
1
x
(
n
)
exp
(
−
j
2
π
N
n
k
)
,
0
≤
k
≤
N
−
1
(1)
X(k) = \sum\limits_{n = 0}^{N - 1} {x(n)\exp ( - j\frac{{2\pi }}{N}nk),0 \le k \le N - 1}\tag{1}
X(k)=n=0∑N−1x(n)exp(−jN2πnk),0≤k≤N−1(1)
我们来研究一下它的计算过程,首先对于一个
k
k
k值来说,
X
(
k
)
=
∑
n
=
0
N
−
1
X(k) = \sum\limits_{n = 0}^{N - 1}
X(k)=n=0∑N−1表示要做
N
−
1
N-1
N−1次的加法,而每一次的加法中都需要做
x
(
n
)
⋅
exp
(
−
j
2
π
N
n
k
)
x(n)\cdot \exp ( - j\frac{{2\pi }}{N}nk)
x(n)⋅exp(−jN2πnk)的乘法运算,总计为
N
N
N次乘法运算。这就意味着
0
≤
k
≤
N
−
1
0 \le k \le N - 1
0≤k≤N−1这个取值范围中
N
N
N个
X
(
k
)
X(k)
X(k)的值共需要
N
2
N^2
N2次的乘法和
N
⋅
(
N
−
1
)
N \cdot (N - 1)
N⋅(N−1)次加法。这样的算法复杂度当
N
N
N取值很大的时候是不可接受的,而优化的出发点就落在
exp
(
−
j
2
π
N
n
k
)
\exp ( - j\frac{{2\pi }}{N}nk)
exp(−jN2πnk)这一项的性质上。
首先定义旋转因子
W
N
n
k
W_N^{nk}
WNnk:
W
N
=
exp
(
−
j
2
π
N
)
,
W
N
n
k
=
exp
(
−
j
2
π
N
n
k
)
(2)
{W_N} = \exp ( - j\frac{{2\pi }}{N}),W_N^{nk} = \exp ( - j\frac{{2\pi }}{N}nk)\tag{2}
WN=exp(−jN2π),WNnk=exp(−jN2πnk)(2)
将(2)式代入(1)式中得
X
(
k
)
=
∑
n
=
0
N
−
1
x
(
n
)
W
N
n
k
,
0
≤
k
≤
N
−
1
(3)
X(k) = \sum\limits_{n = 0}^{N - 1} {x(n)W_N^{nk},0 \le k \le N - 1}\tag{3}
X(k)=n=0∑N−1x(n)WNnk,0≤k≤N−1(3)
旋转因子
W
N
n
k
W_N^{nk}
WNnk的周期性:
W
N
k
n
=
W
N
k
(
n
+
N
)
=
W
N
(
k
+
N
)
n
(4)
W_N^{kn} = W_N^{k(n + N)} = W_N^{(k + N)n}\tag{4}
WNkn=WNk(n+N)=WN(k+N)n(4)
或表示为
W
N
k
n
=
W
N
r
,
r
=
(
n
k
)
m
o
d
N
(5)
W_N^{kn} = W_N^{r} ,r = (nk)\bmod N\tag{5}
WNkn=WNr,r=(nk)modN(5)
以及对称性:
W
N
k
n
+
N
/
2
=
−
W
N
k
n
(6)
W_N^{kn + N/2} = - W_N^{kn}\tag{6}
WNkn+N/2=−WNkn(6)
有了这两个性质之后,设
N
=
2
m
(
m
∈
N
+
)
N = {2^m}(m \in {N^ + })
N=2m(m∈N+)并将方程(3)分解为两部分:
X
(
k
)
=
∑
r
=
0
N
2
−
1
x
(
2
r
)
⋅
W
N
2
r
k
(
e
v
e
n
)
+
∑
r
=
0
N
2
−
1
x
(
2
r
+
1
)
⋅
W
N
(
2
r
+
1
)
k
(
o
d
d
)
(7)
X(k) = \sum\limits_{r = 0}^{\frac{N}{2} - 1} {x(2r) \cdot W_N^{2rk}(even) + } \sum\limits_{r = 0}^{\frac{N}{2} - 1} {x(2r + 1) \cdot W_N^{(2r + 1)k}(odd)} \tag{7}
X(k)=r=0∑2N−1x(2r)⋅WN2rk(even)+r=0∑2N−1x(2r+1)⋅WN(2r+1)k(odd)(7)
其中,偶数序列
(
e
v
e
n
)
(even)
(even)为:
∑
r
=
0
N
2
−
1
x
(
2
r
)
⋅
W
N
2
r
k
(8)
\sum\limits_{r = 0}^{\frac{N}{2} - 1} {x(2r) \cdot W_N^{2rk}}\tag{8}
r=0∑2N−1x(2r)⋅WN2rk(8)
奇数序列
(
o
d
d
)
(odd)
(odd)为:
∑
r
=
0
N
2
−
1
x
(
2
r
+
1
)
⋅
W
N
(
2
r
+
1
)
k
(9)
\sum\limits_{r = 0}^{\frac{N}{2} - 1} {x(2r + 1) \cdot W_N^{(2r + 1)k}}\tag{9}
r=0∑2N−1x(2r+1)⋅WN(2r+1)k(9)
利用周期性与对称性以及把序列分解为奇偶序列(分治及递归的思想),可以将大部分计算(那些反复计算的部分)消除掉,从而能降低与
N
N
N的二次依赖关系,下面的1.2小节通过例子来初步说明优化的原理。
现在,利用一个长度为
N
=
4
N=4
N=4的信号
x
(
n
)
x(n)
x(n)进行优化举例,通过式(3)可以得到:
X
(
k
)
=
∑
n
=
0
4
x
(
n
)
W
4
n
k
,
0
≤
k
≤
3
(10)
X(k) = \sum\limits_{n = 0}^{4} {x(n)W_4^{nk},0 \le k \le 3}\tag{10}
X(k)=n=0∑4x(n)W4nk,0≤k≤3(10)
将该式子展开可以得到:
k
=
0
:
X
(
0
)
=
∑
n
=
0
3
x
(
n
)
⋅
W
4
n
k
=
x
(
0
)
⋅
W
4
0
+
x
(
1
)
⋅
W
4
0
+
x
(
2
)
⋅
W
4
0
+
x
(
3
)
⋅
W
4
0
k
=
1
:
X
(
1
)
=
∑
n
=
0
3
x
(
n
)
⋅
W
4
n
k
=
x
(
0
)
⋅
W
4
0
+
x
(
1
)
⋅
W
4
1
+
x
(
2
)
⋅
W
4
2
+
x
(
3
)
⋅
W
4
3
k
=
2
:
X
(
2
)
=
∑
n
=
0
3
x
(
n
)
⋅
W
4
n
k
=
x
(
0
)
⋅
W
4
0
+
x
(
1
)
⋅
W
4
2
+
x
(
2
)
⋅
W
4
4
+
x
(
3
)
⋅
W
4
6
k
=
3
:
X
(
3
)
=
∑
n
=
0
3
x
(
n
)
⋅
W
4
n
k
=
x
(
0
)
⋅
W
4
0
+
x
(
1
)
⋅
W
4
3
+
x
(
2
)
⋅
W
4
6
+
x
(
3
)
⋅
W
4
9
(11)
\begin{array}{l} k = 0:X(0) = \sum\limits_{n = 0}^3 {x(n) \cdot W_4^{nk} = x(0)} \cdot W_4^0 + x(1) \cdot W_4^0 + x(2) \cdot W_4^0 + x(3) \cdot W_4^0\\ k = 1:X(1) = \sum\limits_{n = 0}^3 {x(n) \cdot W_4^{nk} = x(0)} \cdot W_4^0 + x(1) \cdot W_4^1 + x(2) \cdot W_4^2 + x(3) \cdot W_4^3\\ k = 2:X(2) = \sum\limits_{n = 0}^3 {x(n) \cdot W_4^{nk} = x(0)} \cdot W_4^0 + x(1) \cdot W_4^2 + x(2) \cdot W_4^4 + x(3) \cdot W_4^6\\ k = 3:X(3) = \sum\limits_{n = 0}^3 {x(n) \cdot W_4^{nk} = x(0)} \cdot W_4^0 + x(1) \cdot W_4^3 + x(2) \cdot W_4^6 + x(3) \cdot W_4^9 \end{array}\tag{11}
k=0:X(0)=n=0∑3x(n)⋅W4nk=x(0)⋅W40+x(1)⋅W40+x(2)⋅W40+x(3)⋅W40k=1:X(1)=n=0∑3x(n)⋅W4nk=x(0)⋅W40+x(1)⋅W41+x(2)⋅W42+x(3)⋅W43k=2:X(2)=n=0∑3x(n)⋅W4nk=x(0)⋅W40+x(1)⋅W42+x(2)⋅W44+x(3)⋅W46k=3:X(3)=n=0∑3x(n)⋅W4nk=x(0)⋅W40+x(1)⋅W43+x(2)⋅W46+x(3)⋅W49(11)
将(11)写为矩阵形式为:
[
X
(
0
)
X
(
1
)
X
(
2
)
X
(
3
)
]
=
[
W
4
0
W
4
0
W
4
0
W
4
0
W
4
0
W
4
1
W
4
2
W
4
3
W
4
0
W
4
2
W
4
4
W
4
6
W
4
0
W
4
3
W
4
6
W
4
9
]
⋅
[
x
(
0
)
x
(
1
)
x
(
2
)
x
(
3
)
]
(12)
\left[\begin{array}{c} X(0) \\ X(1) \\ X(2) \\ X(3) \end{array}\right]=\left[\begin{array}{cccc} W_{4}^{0} & W_{4}^{0} & W_{4}^{0} & W_{4}^{0} \\ W_{4}^{0} & W_{4}^{1} & W_{4}^{2} & W_{4}^{3} \\ W_{4}^{0} & W_{4}^{2} & W_{4}^{4} & W_{4}^{6} \\ W_{4}^{0} & W_{4}^{3} & W_{4}^{6} & W_{4}^{9} \end{array}\right] \cdot\left[\begin{array}{c} x(0) \\ x(1) \\ x(2) \\ x(3) \end{array}\right]\tag{12}
⎣⎢⎢⎡X(0)X(1)X(2)X(3)⎦⎥⎥⎤=⎣⎢⎢⎡W40W40W40W40W40W41W42W43W40W42W44W46W40W43W46W49⎦⎥⎥⎤⋅⎣⎢⎢⎡x(0)x(1)x(2)x(3)⎦⎥⎥⎤(12)
现在可以使用式(5)和式(6)来简化式(12)中的
W
4
n
k
W_4^{nk}
W4nk矩阵。
利用式(5)能推导得到:
W
N
m
N
=
W
N
0
=
1
(13)
W_N^{mN}=W_N^{0}=1\tag{13}
WNmN=WN0=1(13)
这样式(12)中有:
W
4
4
=
W
4
0
=
1
(14)
W_4^{4}=W_4^{0}=1\tag{14}
W44=W40=1(14)
经过简化后式(12)的
W
4
n
k
W_4^{nk}
W4nk矩阵为:
W
4
n
k
=
[
1
1
1
1
1
W
4
1
W
4
2
W
4
3
1
W
4
2
1
W
4
6
1
W
4
3
W
4
6
W
4
9
]
(15)
W_4^{nk}=\left[\begin{array}{cccc} 1 & 1 & 1 & 1\\ 1 & W_{4}^{1} & W_{4}^{2} & W_{4}^{3} \\ 1 & W_{4}^{2} & 1 & W_{4}^{6} \\ 1 & W_{4}^{3} & W_{4}^{6} & W_{4}^{9} \end{array}\right\tag{15}]
W4nk=⎣⎢⎢⎡11111W41W42W431W421W461W43W46W49⎦⎥⎥⎤(15)
利用周期性式(5)推导可得:
W
4
6
=
W
4
2
,
W
4
9
=
W
4
1
(16)
W_4^{6}=W_4^{2},W_4^{9}=W_4^{1}\tag{16}
W46=W42,W49=W41(16)
再利用对称性式(6)推导得到:
W
4
2
=
−
W
4
0
=
−
1
,
W
4
3
=
−
W
4
1
(17)
W_4^{2}=-W_4^{0}=-1,W_4^{3}=-W_4^{1}\tag{17}
W42=−W40=−1,W43=−W41(17)
由式(16)及(17)化简式(15)得:
W
4
n
k
=
[
1
1
1
1
1
W
4
1
−
1
−
W
4
1
1
−
1
1
−
1
1
−
W
4
1
−
1
W
4
1
]
(18)
W_4^{nk}=\left[\begin{array}{cccc} 1 & 1 & 1 & 1\\ 1 & W_{4}^{1} & -1 & -W_{4}^{1} \\ 1 & -1 & 1 & -1 \\ 1 & -W_{4}^{1} & -1 & W_{4}^{1} \end{array}\right\tag{18}]
W4nk=⎣⎢⎢⎡11111W41−1−W411−11−11−W41−1W41⎦⎥⎥⎤(18)
现在调换矢量
x
⃗
=
[
x
(
0
)
x
(
1
)
x
(
2
)
x
(
3
)
]
T
\vec x =\left[\begin{array}{cccc} {x(0)} & {x(1)}& {x(2)}& {x(3)} \end{array}\right]^{T}
x
=[x(0)x(1)x(2)x(3)]T的第二行和第三行,与此同时调换
W
4
n
k
W_4^{nk}
W4nk矩阵的第二列和第三列,得到
[
X
(
0
)
X
(
1
)
X
(
2
)
X
(
3
)
]
=
[
1
1
1
1
1
−
1
W
4
1
−
W
4
1
1
1
−
1
−
1
1
−
1
−
W
4
1
W
4
1
]
⋅
[
x
(
0
)
x
(
2
)
x
(
1
)
x
(
3
)
]
(19)
\left[\begin{array}{c} X(0) \\ X(1) \\ X(2) \\ X(3) \end{array}\right]=\left[\begin{array}{cccc} 1 & 1 & 1 & 1\\ 1 & -1 & W_{4}^{1} & -W_{4}^{1} \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -W_{4}^{1} & W_{4}^{1} \end{array}\right] \cdot\left[\begin{array}{c} x(0) \\ x(2) \\ x(1) \\ x(3) \end{array}\right]\tag{19}
⎣⎢⎢⎡X(0)X(1)X(2)X(3)⎦⎥⎥⎤=⎣⎢⎢⎡11111−11−11W41−1−W411−W41−1W41⎦⎥⎥⎤⋅⎣⎢⎢⎡x(0)x(2)x(1)x(3)⎦⎥⎥⎤(19)
现定义
W
~
4
n
k
=
[
1
1
1
1
1
−
1
W
4
1
−
W
4
1
1
1
−
1
−
1
1
−
1
−
W
4
1
W
4
1
]
(20)
\tilde W_4^{nk}=\left[\begin{array}{cccc} 1 & 1 & 1 & 1\\ 1 & -1 & W_{4}^{1} & -W_{4}^{1} \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -W_{4}^{1} & W_{4}^{1} \end{array}\right] \tag{20}
W~4nk=⎣⎢⎢⎡11111−11−11W41−1−W411−W41−1W41⎦⎥⎥⎤(20)
对
W
~
4
n
k
\tilde W_4^{nk}
W~4nk进行分块:

对矢量
x
⃗
\vec x
x
进行分块:
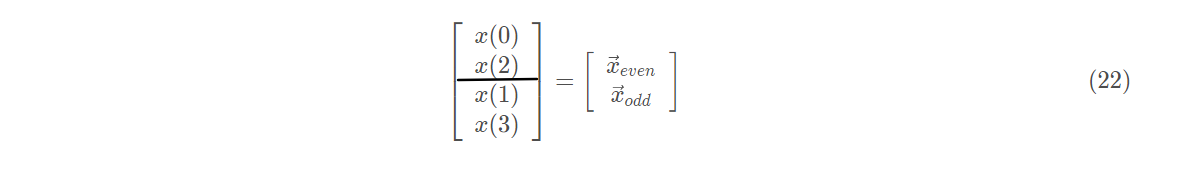
将式(21)和(22)代入式(19)中有:
[
X
(
0
)
X
(
1
)
X
(
2
)
X
(
3
)
]
=
[
A
B
C
D
]
⋅
[
x
⃗
e
v
e
n
x
⃗
o
d
d
]
=
[
A
⋅
x
⃗
e
v
e
n
+
B
⋅
x
⃗
o
d
d
C
⋅
x
⃗
e
v
e
n
+
D
⋅
x
⃗
o
d
d
]
(23)
\left[\begin{array}{c} X(0) \\ X(1) \\ X(2) \\ X(3) \end{array}\right]=\left[\begin{array}{cccc} A & B \\ C & D \end{array}\right] \cdot\left[\begin{array}{c} \vec x_{even} \\ \vec x_{odd} \\ \end{array}\right]=\left[\begin{array}{c} A\cdot\vec x_{even}+ B\cdot\vec x_{odd}\\ C\cdot\vec x_{even} +D\cdot\vec x_{odd}\\ \end{array}\right]\tag{23}
⎣⎢⎢⎡X(0)X(1)X(2)X(3)⎦⎥⎥⎤=[ACBD]⋅[x
evenx
odd]=[A⋅x
even+B⋅x
oddC⋅x
even+D⋅x
odd](23)
显然,矩阵
A
,
C
A,C
A,C只与矢量
x
⃗
e
v
e
n
\vec x_{even}
x
even有关,而矩阵
B
,
D
B,D
B,D只与矢量
x
⃗
o
d
d
\vec x_{odd}
x
odd有关。
根据式(23),将矩阵方程式(19)写成方程组的形式:
k
=
0
:
X
(
0
)
=
x
(
0
)
+
x
(
2
)
+
x
(
1
)
+
x
(
3
)
k
=
1
:
X
(
1
)
=
x
(
0
)
−
x
(
2
)
+
W
4
1
(
x
(
1
)
−
x
(
3
)
)
k
=
2
:
X
(
2
)
=
x
(
0
)
+
x
(
2
)
−
(
x
(
1
)
+
x
(
3
)
)
k
=
3
:
X
(
3
)
=
x
(
0
)
−
x
(
2
)
−
W
4
1
(
x
(
1
)
−
x
(
3
)
)
(24)
\begin{gathered} k=0: X(0)=x(0)+x(2)+x(1)+x(3) \\ k=1: X(1)=x(0)-x(2)+W_{4}^{1}(x(1)-x(3)) \\ k=2: X(2)=x(0) +x(2)-(x(1)+x(3)) \\ k=3: X(3)=x(0)-x(2)-W_{4}^{1}(x(1)-x(3)) \end{gathered}\tag{24}
k=0:X(0)=x(0)+x(2)+x(1)+x(3)k=1:X(1)=x(0)−x(2)+W41(x(1)−x(3))k=2:X(2)=x(0)+x(2)−(x(1)+x(3))k=3:X(3)=x(0)−x(2)−W41(x(1)−x(3))(24)
现在定义
x
(
0
)
+
x
(
2
)
=
G
(
0
)
x
(
1
)
+
x
(
3
)
=
H
(
0
)
x
(
0
)
−
x
(
2
)
=
G
(
1
)
x
(
1
)
−
x
(
3
)
=
H
(
1
)
(25)
\begin{aligned} &x(0)+x(2)=G(0) \\ &x(1)+x(3)=H(0) \\ &x(0)-x(2)=G(1) \\ &x(1)-x(3)=H(1) \end{aligned}\tag{25}
x(0)+x(2)=G(0)x(1)+x(3)=H(0)x(0)−x(2)=G(1)x(1)−x(3)=H(1)(25)
将式(25)代入到式(24)可以得到:
k
=
0
:
X
(
0
)
=
G
(
0
)
+
H
(
0
)
k
=
1
:
X
(
1
)
=
G
(
1
)
+
W
4
1
H
(
1
)
k
=
2
:
X
(
2
)
=
G
(
0
)
−
H
(
0
)
k
=
3
:
X
(
3
)
=
G
(
1
)
−
W
4
1
H
(
1
)
(26)
\begin{gathered} k=0: X(0)=G(0)+H(0) \\ k=1: X(1)=G(1)+W_{4}^{1} H(1) \\ k=2: X(2)=G(0)-H(0) \\ k=3: X(3)=G(1)-W_{4}^{1} H(1) \end{gathered}\tag{26}
k=0:X(0)=G(0)+H(0)k=1:X(1)=G(1)+W41H(1)k=2:X(2)=G(0)−H(0)k=3:X(3)=G(1)−W41H(1)(26)
由式(25)我们可以知道,中间变量
G
(
0
)
,
H
(
0
)
,
G
(
1
)
,
H
(
0
)
G(0),H(0),G(1),H(0)
G(0),H(0),G(1),H(0)都是通过一次加法计算得到,而通过式(26)又可以知道
X
(
0
)
,
X
(
1
)
X(0),X(1)
X(0),X(1),
X
(
2
)
,
X
(
3
)
X(2),X(3)
X(2),X(3)各是通过一次加法得到的。简化后,一个
N
=
4
N=4
N=4长度的序列的加法次数为
8
8
8次,而简化之前则要
4
⋅
(
4
−
1
)
=
12
4\cdot(4-1)=12
4⋅(4−1)=12次加法。见式(26)的右边,乘法只需要做
4
4
4次分别如下所示:
H
(
0
)
,
W
4
1
H
(
1
)
,
−
H
(
0
)
,
−
W
4
1
H
(
1
)
(27)
H(0),W_{4}^{1} H(1),-H(0),-W_{4}^{1} H(1)\tag{27}
H(0),W41H(1),−H(0),−W41H(1)(27)
可见,获得中间变量
G
,
H
G,H
G,H的过程中是没有进行乘法运算的,相比于简化之前的
4
⋅
4
=
16
4\cdot4=16
4⋅4=16显著是减少的。
从以上的例子可以知道,优化的原理主要是①通过周期性和对称性减少旋转因子 W N n k W_N^{nk} WNnk的计算次数;②通过奇偶分解的分治思想以及设置中间变量减少计算次数。以下第二节是基-2FFT算法的推导。
此次的推导过程主要参考《数字信号处理——原理、算法与应用(第四版)》的P385-388。若对推导的过程没有兴趣或存在疑惑,可以直接看第3节的实现代码。推导的是按时间抽取的FFT(DIT - FFT)算法,另外一种实现的角度则是按频率抽取( DlF-FFT )算法。
首先证明一个恒等式
W
N
2
r
k
=
W
N
/
2
r
k
W_N^{2rk}=W_{N/2}^{rk}
WN2rk=WN/2rk:
W
N
2
r
k
=
exp
(
−
j
2
π
N
2
r
k
)
=
exp
(
−
j
2
π
N
/
2
r
k
)
=
W
N
/
2
r
k
(28)
W_N^{2rk}=\exp ( - j\frac{{2\pi }}{N}2rk) = \exp ( - j\frac{{2\pi }}{{N/2}}rk) = W_{N/2}^{rk}\tag{28}
WN2rk=exp(−jN2π2rk)=exp(−jN/22πrk)=WN/2rk(28)
并把
N
N
N点数据序列抽取分成两个长度为
N
/
2
N/2
N/2的奇偶子序列
f
1
(
n
)
f_1(n)
f1(n)和
f
2
(
n
)
f_2(n)
f2(n):
f
1
(
n
)
=
x
(
2
n
)
f
2
(
n
)
=
x
(
2
n
+
1
)
,
0
≤
n
≤
N
/
2
−
1
(29)
\begin{array}{l} {f_1}(n) = x(2n)\\ {f_2}(n) = x(2n + 1),0 \le n \le N/2 - 1 \end{array}\tag{29}
f1(n)=x(2n)f2(n)=x(2n+1),0≤n≤N/2−1(29)
把式(28)和式(29)代入式(7)中得到:
X
(
k
)
=
∑
r
=
0
N
2
−
1
f
1
(
r
)
⋅
W
N
/
2
r
k
+
W
N
k
∑
r
=
0
N
2
−
1
f
2
(
r
)
⋅
W
N
/
2
r
k
=
F
1
(
k
)
+
W
N
k
F
2
(
k
)
,
0
≤
k
≤
N
−
1
(30)
\begin{array}{c} X(k) = \sum\limits_{r = 0}^{\frac{N}{2} - 1} {{f_1}(r) \cdot W_{N/2}^{rk} + } W_N^k\sum\limits_{r = 0}^{\frac{N}{2} - 1} {{f_2}(r) \cdot W_{N/2}^{rk}} \\ = {F_1}(k) + W_N^k{F_2}(k),0 \le k \le N - 1 \end{array}\tag{30}
X(k)=r=0∑2N−1f1(r)⋅WN/2rk+WNkr=0∑2N−1f2(r)⋅WN/2rk=F1(k)+WNkF2(k),0≤k≤N−1(30)
其中,
F
1
(
k
)
F_1(k)
F1(k)和
F
2
(
k
)
F_2(k)
F2(k)分别是序列
f
1
(
r
)
f_1(r)
f1(r)和
f
2
(
r
)
f_2(r)
f2(r)的长度为
N
/
2
N/2
N/2的DFT,这样
n
n
n的取值范围可以从
N
N
N缩小一半为
N
/
2
N/2
N/2。
因为
F
1
(
k
)
F_1(k)
F1(k)和
F
2
(
k
)
F_2(k)
F2(k)是周期性的,周期为
N
/
2
N/2
N/2,所以我们有
F
1
(
k
+
N
/
2
)
=
F
(
k
)
F_1(k+N/2)=F(k)
F1(k+N/2)=F(k)和
F
2
(
k
+
N
/
2
)
=
F
(
k
)
F_2(k+N/2)=F(k)
F2(k+N/2)=F(k)。此外,由于旋转因子
W
N
k
+
N
/
2
=
−
W
N
k
W_N^{k+N/2}=-W_N^{k}
WNk+N/2=−WNk,k的取值范围可以从
N
N
N缩小一半为
N
/
2
N/2
N/2。所以式(30)可以表示为
X
(
k
)
=
F
1
(
k
)
+
W
N
k
F
2
(
k
)
,
k
=
0
,
1
,
⋯
,
N
2
−
1
X
(
k
+
N
2
)
=
F
1
(
k
)
−
W
N
k
F
2
(
k
)
,
k
=
0
,
1
,
⋯
,
N
2
−
1
(31)
\begin{gathered} X(k)=F_{1}(k)+W_{N}^{k} F_{2}(k), \quad k=0,1, \cdots, \frac{N}{2}-1 \\ X\left(k+\frac{N}{2}\right)=F_{1}(k)-W_{N}^{k} F_{2}(k), \quad k=0,1, \cdots, \frac{N}{2}-1 \end{gathered}\tag{31}
X(k)=F1(k)+WNkF2(k),k=0,1,⋯,2N−1X(k+2N)=F1(k)−WNkF2(k),k=0,1,⋯,2N−1(31)
现在算一下分解后所需的总乘法数:通过式(31)可以观察到计算
F
1
(
k
)
F_1(k)
F1(k)与
F
2
(
k
)
F_2(k)
F2(k)各需要
(
N
/
2
)
2
(N/2)^{2}
(N/2)2次乘法。此外,计算
W
N
k
F
2
(
k
)
W_{N}^{k} F_{2}(k)
WNkF2(k)需要
N
/
2
N/2
N/2次复数乘法。所以,计算
X
(
k
)
X(k)
X(k)共需要
2
(
N
/
2
)
2
+
N
/
2
=
N
2
/
2
+
N
/
2
2(N/2)^{2}+N/2=N^{2}/2+N/2
2(N/2)2+N/2=N2/2+N/2次复数乘法。由此可见,第一步就将算法中的乘法的次数由
N
2
N^{2}
N2降到
N
2
/
2
+
N
/
2
N^{2}/2+N/2
N2/2+N/2。
与前面1.2小节中的式(26)一样,定义中间变量:
G
1
(
k
)
=
F
1
(
k
)
,
k
=
0
,
1
,
⋯
,
N
2
−
1
G
2
(
k
)
=
W
N
k
F
2
(
k
)
,
k
=
0
,
1
,
⋯
,
N
2
−
1
(32)
\begin{array}{ll} G_{1}(k)=F_{1}(k), & k=0,1, \cdots, \frac{N}{2}-1 \\ G_{2}(k)=W_{N}^{k} F_{2}(k), & k=0,1, \cdots, \frac{N}{2}-1 \end{array}\tag{32}
G1(k)=F1(k),G2(k)=WNkF2(k),k=0,1,⋯,2N−1k=0,1,⋯,2N−1(32)
由此式(31)可以改写为
X
(
k
)
=
G
1
(
k
)
+
G
2
(
k
)
,
k
=
0
,
1
,
⋯
,
N
2
−
1
X
(
k
+
N
2
)
=
G
1
(
k
)
−
G
2
(
k
)
,
k
=
0
,
1
,
⋯
,
N
2
−
1
(33)
\begin{aligned} X(k)=G_{1}(k)+G_{2}(k), & k=0,1, \cdots, \frac{N}{2}-1 \\ X\left(k+\frac{N}{2}\right)=G_{1}(k)-G_{2}(k), & k=0,1, \cdots, \frac{N}{2}-1 \end{aligned}\tag{33}
X(k)=G1(k)+G2(k),X(k+2N)=G1(k)−G2(k),k=0,1,⋯,2N−1k=0,1,⋯,2N−1(33)
以此类推,对
f
1
(
n
)
f_1(n)
f1(n)与
f
2
(
n
)
f_2(n)
f2(n)分别重复上述原序列
x
(
n
)
x(n)
x(n)的抽取过程,则
f
1
(
n
)
f_1(n)
f1(n)会产生两个长度为
N
/
4
N/4
N/4的序列:
v
11
(
n
)
=
f
1
(
2
n
)
,
n
=
0
,
1
,
⋯
,
N
4
−
1
v
12
(
n
)
=
f
1
(
2
n
+
1
)
,
n
=
0
,
1
,
⋯
,
N
4
−
1
(34)
\begin{array}{ll} v_{11}(n)=f_{1}(2 n), & n=0,1, \cdots, \frac{N}{4}-1 \\ v_{12}(n)=f_{1}(2 n+1), & n=0,1, \cdots, \frac{N}{4}-1 \end{array}\tag{34}
v11(n)=f1(2n),v12(n)=f1(2n+1),n=0,1,⋯,4N−1n=0,1,⋯,4N−1(34)
同理,
f
2
(
n
)
f_2(n)
f2(n)将产生
v
21
(
n
)
=
f
2
(
2
n
)
,
n
=
0
,
1
,
⋯
,
N
4
−
1
v
22
(
n
)
=
f
2
(
2
n
+
1
)
,
n
=
0
,
1
,
⋯
,
N
4
−
1
(34)
\begin{array}{ll} v_{21}(n)=f_{2}(2 n), & n=0,1, \cdots, \frac{N}{4}-1 \\ v_{22}(n)=f_{2}(2 n+1), & n=0,1, \cdots, \frac{N}{4}-1 \end{array}\tag{34}
v21(n)=f2(2n),v22(n)=f2(2n+1),n=0,1,⋯,4N−1n=0,1,⋯,4N−1(34)
同式(31),可以分别计算
N
/
2
N/2
N/2点DFT
F
1
(
k
)
F_1(k)
F1(k)和
F
2
(
k
)
F_2(k)
F2(k)
F
1
(
k
)
=
V
11
(
k
)
+
W
N
/
2
k
V
12
(
k
)
,
k
=
0
,
1
,
⋯
,
N
4
−
1
F
1
(
k
+
N
4
)
=
V
11
(
k
)
−
W
N
/
2
k
V
12
(
k
)
,
k
=
0
,
1
,
⋯
,
N
4
−
1
F
2
(
k
)
=
V
21
(
k
)
+
W
N
/
2
k
V
22
(
k
)
,
k
=
0
,
1
,
⋯
,
N
4
−
1
F
2
(
k
+
N
4
)
=
V
21
(
k
)
−
W
N
/
2
k
V
22
(
k
)
,
k
=
0
,
1
,
⋯
,
N
4
−
1
(35)
\begin{aligned} F_{1}(k) &=V_{11}(k)+W_{N / 2}^{k} V_{12}(k), & & k=0,1, \cdots, \frac{N}{4}-1 \\ F_{1}\left(k+\frac{N}{4}\right) &=V_{11}(k)-W_{N / 2}^{k} V_{12}(k), & & k=0,1, \cdots, \frac{N}{4}-1 \\ F_{2}(k) &=V_{21}(k)+W_{N / 2}^{k} V_{22}(k), & & k=0,1, \cdots, \frac{N}{4}-1 \\ F_{2}\left(k+\frac{N}{4}\right) &=V_{21}(k)-W_{N / 2}^{k} V_{22}(k), & & k=0, 1,\cdots, \frac{N}{4}-1 \end{aligned}\tag{35}
F1(k)F1(k+4N)F2(k)F2(k+4N)=V11(k)+WN/2kV12(k),=V11(k)−WN/2kV12(k),=V21(k)+WN/2kV22(k),=V21(k)−WN/2kV22(k),k=0,1,⋯,4N−1k=0,1,⋯,4N−1k=0,1,⋯,4N−1k=0,1,⋯,4N−1(35)
其中,{
V
i
j
(
k
)
V_{ij}(k)
Vij(k)}序列是{
v
i
j
(
n
)
v_{ij}(n)
vij(n)}序列的
N
/
4
N/4
N/4点DFT。
观察式(35)可知{ V i j ( k ) V_{ij}(k) Vij(k)}序列的计算共需 4 ( N / 4 ) 2 = N 2 / 4 4(N/4)^{2}=N^2/4 4(N/4)2=N2/4次乘法,故计算 F 1 ( k ) F_1(k) F1(k)和 F 2 ( k ) F_2(k) F2(k)的计算共需 N 2 / 4 + N / 2 N^2/4+N/2 N2/4+N/2次复数乘法,而利用 F 1 ( k ) F_1(k) F1(k)和 F 2 ( k ) F_2(k) F2(k)来计算 X ( k ) X(k) X(k)需额外的 N / 2 N/2 N/2次复数乘法。可见总需要的复数乘法次数为 N 2 / 4 + N N^2/4+N N2/4+N,比上一次抽取所需的总乘法数 N 2 / 2 + N / 2 N^{2}/2+N/2 N2/2+N/2少了一半。
数据序列的抽取可以不断重复,直到导致的序列简化为1点序列,根据式(3)计算可得,1点序列的DFT结果为本身,故抽取到只有1点的序列时直接可以当成DFT结果并进行递归计算。对于 N = 2 m N=2^{m} N=2m的序列,这种抽取可执行 log 2 N \log _2^N log2N次。
对于第i次抽取后,计算抽取后各子序列
H
i
j
(
k
)
H_{ij}(k)
Hij(k)的DFT的通式。(其中
i
i
i代表第
i
i
i次抽取或称为第
i
i
i级,
j
j
j代表某次抽取中第
j
j
j个子序列),比如对应式(35)中的第一次抽取的子序列就可以表示为
H
11
(
k
)
=
F
1
(
k
)
,
H
12
(
k
)
=
F
2
(
k
)
H_{11}(k)=F_1(k),H_{12}(k)=F_2(k)
H11(k)=F1(k),H12(k)=F2(k)以及第二次抽取:
H
21
(
k
)
=
V
11
(
k
)
,
H
22
(
k
)
=
V
12
(
k
)
,
H
23
(
k
)
=
V
21
(
k
)
,
H
24
(
k
)
=
V
22
(
k
)
H_{21}(k)=V_{11}(k),H_{22}(k)=V_{12}(k),H_{23}(k)=V_{21}(k),H_{24}(k)=V_{22}(k)
H21(k)=V11(k),H22(k)=V12(k),H23(k)=V21(k),H24(k)=V22(k)。由此统一符号后各子序列
H
i
j
(
k
)
H_{ij}(k)
Hij(k)的DFT的通式为
H
i
j
(
k
)
=
H
(
i
+
1
)
j
1
(
k
)
+
W
N
/
(
2
i
−
1
)
k
H
(
i
+
1
)
j
2
(
k
)
,
k
=
0
,
1
,
⋯
,
N
2
i
−
1
H
i
j
(
k
+
N
2
i
)
=
H
(
i
+
1
)
j
1
(
k
)
−
W
N
/
(
2
i
−
1
)
k
H
(
i
+
1
)
j
2
(
k
)
,
k
=
0
,
1
,
⋯
,
N
2
i
−
1
(36)
\begin{aligned} H_{ij}(k) &=H_{(i+1)j_1}(k)+W_{N / (2^{i-1})}^{k} H_{(i+1)j_2}(k), & & k=0,1, \cdots, \frac{N}{2^{i}}-1 \\ H_{ij}\left(k+\frac{N}{2^{i}}\right) &=H_{(i+1)j_1}(k)-W_{N / (2^{i-1})}^{k} H_{(i+1)j_2}(k), & & k=0,1, \cdots, \frac{N}{2^{i}}-1 \\ \end{aligned}\tag{36}
Hij(k)Hij(k+2iN)=H(i+1)j1(k)+WN/(2i−1)kH(i+1)j2(k),=H(i+1)j1(k)−WN/(2i−1)kH(i+1)j2(k),k=0,1,⋯,2iN−1k=0,1,⋯,2iN−1(36)
通过式(28)恒等式可以得到
W
N
/
(
2
i
−
1
)
k
=
W
N
(
k
⋅
2
i
−
1
)
(37)
W_{N / (2^{i-1})}^{k}=W_{N}^{(k\cdot 2^{i-1})}\tag{37}
WN/(2i−1)k=WN(k⋅2i−1)(37)
将式(37)代入带式(36)中得
H
i
j
(
k
)
=
H
(
i
+
1
)
j
1
(
k
)
+
W
N
(
k
⋅
2
i
−
1
)
H
(
i
+
1
)
j
2
(
k
)
,
k
=
0
,
1
,
⋯
,
N
2
i
−
1
H
i
j
(
k
+
N
2
i
)
=
H
(
i
+
1
)
j
1
(
k
)
−
W
N
(
k
⋅
2
i
−
1
)
H
(
i
+
1
)
j
2
(
k
)
,
k
=
0
,
1
,
⋯
,
N
2
i
−
1
(38)
\begin{aligned} H_{ij}(k) &=H_{(i+1)j_1}(k)+W_{N}^{(k\cdot 2^{i-1})} H_{(i+1)j_2}(k), & & k=0,1, \cdots, \frac{N}{2^{i}}-1 \\ H_{ij}\left(k+\frac{N}{2^{i}}\right) &=H_{(i+1)j_1}(k)-W_{N}^{(k\cdot 2^{i-1})} H_{(i+1)j_2}(k), & & k=0,1, \cdots, \frac{N}{2^{i}}-1 \\ \end{aligned}\tag{38}
Hij(k)Hij(k+2iN)=H(i+1)j1(k)+WN(k⋅2i−1)H(i+1)j2(k),=H(i+1)j1(k)−WN(k⋅2i−1)H(i+1)j2(k),k=0,1,⋯,2iN−1k=0,1,⋯,2iN−1(38)
其中,
j
1
j_1
j1和
j
2
j_2
j2分别是第
j
j
j个子序列分解后下一次抽取的两个子序列,注意到每一次
j
j
j的取值范围总是每
i
i
i次抽取的两倍。整个过程就叫做按时间抽取的FFT(DIT - FFT)算法。
观察通式(38),可以定义以下的基本运算,如下图所示:

其中 W N r = W N ( k ⋅ 2 i − 1 ) W_N^{r}=W_{N}^{(k\cdot 2^{i-1})} WNr=WN(k⋅2i−1),中间变量 a = H ( i + 1 ) j 1 ( k ) a=H_{(i+1)j_1}(k) a=H(i+1)j1(k)以及 b = H ( i + 1 ) j 2 ( k ) b=H_{(i+1)j_2}(k) b=H(i+1)j2(k),所得的结果 A = H i j ( k ) A=H_{ij}(k) A=Hij(k), B = H i j ( k + N 2 i ) B=H_{ij}\left(k+\frac{N}{2^{i}}\right) B=Hij(k+2iN),正好与式(38)对应上了。这种运算称为蝶形运算,因为它的流图看起来像是一只蝴蝶。可以看见 W N r b = W N ( k ⋅ 2 i − 1 ) H ( i + 1 ) j 2 ( k ) W_N^{r}b=W_{N}^{(k\cdot 2^{i-1})} H_{(i+1)j_2}(k) WNrb=WN(k⋅2i−1)H(i+1)j2(k)重复出现了两次,故在蝶形运算输入 b b b后直接乘上 W N r W_N^{r} WNr(相等于提前计算好该项)当成一端的输入,这样可以减少一次复数乘法的计算,由此每一次抽取即每一级的乘法运算次数由 N N N减少一半变为 N / 2 N/2 N/2。此外,一般旋转因子 W N r W_N^{r} WNr可以提前算好存在存储中,用到时直接给出索引 r r r值即可调用。
蝶型单元具有以下特点:
以
N
=
8
N=8
N=8的有限长序列举例(1.2小节中
N
=
4
N=4
N=4序列的抽取过程也类似),其抽取的整个过程如下图所示:

上图中,每一个红框表示一个抽取出来的子序列。对每一个序列进行抽取时序号都要重新从0开始数起,再进行奇偶分解。比如对于序列{
x
(
0
)
,
x
(
2
)
,
x
(
4
)
,
x
(
6
)
x(0),x(2),x(4),x(6)
x(0),x(2),x(4),x(6)}分解为相较于它的奇序列{
x
(
0
)
,
x
(
4
)
x(0),x(4)
x(0),x(4)}及偶序列{
x
(
2
)
,
x
(
6
)
x(2),x(6)
x(2),x(6)}。
其往回递归计算过程如下图所示:

如果我们将未抽取之前的序号和抽取完成之后的序号进行二进制编码可以得到:

我们可以看出用红色标记出的二进制编码实际上是进行了码位倒置(实际上没用红色标记的二进制编码也进行了码位倒置,之后倒置前后结果一致)。所以说,对于一个 N = 8 N=8 N=8 的序列来讲,未抽取之前的序号和抽取完成之后的序号在二进制上来讲实际上是发生了码位倒置。故第3节算法实现的开始直接对序列进行码位倒置。
一般来说,每次蝶形运算包括一次复数乘法和两次复数加法,对于 N = 2 m N=2^{m} N=2m的序列,每一个阶段有 N / 2 N/2 N/2次蝶形运算,其有 log 2 N \log _2^N log2N个阶段,所以,正如上面指出的那样,其需 ( N / 2 ) log 2 N (N/2)\log _2^N (N/2)log2N次复数乘法以及 N log 2 N N\log _2^N Nlog2N次复数加法。
一旦对复数 ( a , b ) (a,b) (a,b)执行了产生 ( A , B ) (A,B) (A,B)的蝶形运算,就无须再保存 ( a , b ) (a,b) (a,b)。所以,我们可以将结果 ( A , B ) (A,B) (A,B)保存在与 ( a , b ) (a,b) (a,b)相同的位置。从而,为了存储每个阶段的计算结果( N N N个复数),我们需要一个固定大小的存储空间,如 2 N 2N 2N个寄存器。因为在计算 N N N点FFT的过程中均使用了相同的 2 N 2N 2N个存储位置,所以我们说计算在原位进行。
FFT算法实现的流程图:

FFT算法的matlab实现代码如下,实现的各个变量主要根据式(38)的逆过程进行设置。此外,一般旋转因子
W
N
r
W_N^{r}
WNr可以提前算好存在存储中,用到时直接给出索引
r
r
r值即可调用,但本次实现为了实现简便并没有提前算好旋转因子
W
N
r
W_N^{r}
WNr,而是在循环中实时计算,在一定程度上降低了实现的FFT的运行效率。
function [re_vector] = my_FFT(vector)
%my_FFT 快速傅里叶变换(时域抽取算法)
% 此处显示详细说明
N = length(vector); %获得数据点的个数
%%以下是位反转的实现(时域分解)
re_vector = zeros(1,N); %创建零向量来接收数据
Nbit = log2(N); %二进制位数
for n=1:N
tmp=bit_reverse(n-1,Nbit); %对每一个数进行反转
re_vector(n)=vector(tmp+1);%反转后赋值
end
%%以下实现FFT中的三个循环(频域合成)
step = log2(N); %分解的步数
for n=1:step
group = N/2^n; %分组数
butterfly = N / (group * 2); %每一组要进行蝶形运算的次数
index = 1; %索引初始化
for b=1:group
for k=1:butterfly
r = 2^(step-n)*(k-1); %旋转相位因子
W_r = exp(i*(-2*pi*r/N)); %旋转因子
even = re_vector(index); %偶分组部分
odd = re_vector(index+butterfly)*W_r; %奇分组部分
%赋值
re_vector(index) = even + odd;
re_vector(index+butterfly)= even - odd;
index = index + 1; %分组内索引递增
end
index = 1 + 2 * b * butterfly; %索引组号递增
end
end
end
对应的IFFT(逆快速傅里叶变换)的matlab是实现代码如下,其流程与上述代码一样,只是旋转因子 W N r W_N^{r} WNr要改为 − W N r -W_N^{r} −WNr以及最后得到的结果要乘上 1 / N 1/N 1/N。
function [re_vector] = my_IFFT(vector)
%my_IFFT 快速傅里叶变换(时域抽取算法)
% 此处显示详细说明
N = length(vector); %获得数据点的个数
%%以下是位反转的实现(时域分解)
re_vector = zeros(1,N); %创建零向量来接收数据
Nbit = log2(N); %二进制位数
for n=1:N
tmp=bit_reverse(n-1,Nbit); %对每一个数进行反转
re_vector(n)=vector(tmp+1);%反转后赋值
end
%%以下实现IFFT中的三个循环(频域合成)
step = log2(N); %分解的步数
for n=1:step
group = N/2^n; %分组数
butterfly = N / (group * 2); %每一组要进行蝶形运算的次数
index = 1; %索引初始化
for b=1:group
for k=1:butterfly
r = 2^(step-n)*(k-1); %旋转相位因子
W_r = exp(i*(2*pi*r/N)); %旋转因子
even = re_vector(index); %偶分组部分
odd = re_vector(index+butterfly)*W_r; %奇分组部分
%赋值
re_vector(index) = even + odd;
re_vector(index+butterfly)= even - odd;
re_vector(index) = even + odd;
re_vector(index+butterfly)= even - odd;
index = index + 1; %分组内索引递增
end
index = 1 + 2 * b * butterfly; %索引组号递增
end
end
re_vector = re_vector/N; %最后的结果乘上缩减因子1/N(不要在上面循环里面乘,这样就会乘多次了)
end
与数字信号处理知识点总结(三):离散傅里叶变换(DFT)第5节中实现的方法一样,使用重叠保留法实现线性卷积。唯一不同的是,频域方法中的DFT换成FFT实现,可大大提高线性卷积的速度。实现的代码如下:
function [y] = hsolpsav( x,h,N)
%High-speed O飞rerlap-Save method of block convolutions using FFT
% -------一- ---------- -一- -- - ---------------
%[y]= hsolpsav(x,h,N)
% y = output sequence
% x = input sequence
% h = impulse r esponse
% N = block length (must be a power of two)
N = 2^(ceil(log10(N)/log10(2)));
Lenx = length(x);M = length(h);M1 = M - 1;L = N-M1;
h = fft(h,N); %先做好FFT变换
%
x = [zeros(1,M1),x,zeros(1,N-1)];
K = floor((Lenx+M1-1)/L);
Y = zeros(K+1,N);
% convolution wi th succesive blocks
for k=0:K
xk = fft(x(k*L+1:k*L+N));
Y(k+1,:) = ifft(xk.*h);
end
Y = Y(:,M:N)';
y = (Y(:))';
end
1.[知乎[精品讲义]—快速傅里叶变换(Fast Fourier Transformation)]:https://zhuanlan.zhihu.com/p/110897470?ivk_sa=1024320u
2.John G. Proakis, Dimitris G. Manolakis. 数字信号处理——原理、算法与应用(第四版)[M]. 电子工业出版社,2014.8
3.Steven W. Smith. 实用数字信号处理[M]. 人民邮电出版社,2010.12
4.[美]纳•K•英格尔,[美]约翰•G•普罗克斯. 数字信号处理(MATLAB版)(第3版)[M].西安交通大学出版社,2013.7
