多智能体一致性(Consensus)中的矩阵理论(Matrix Theory)

写在前面

最近在看一些分布式优化的文章，但是大部分文章都是用的离散时间算法。我之前一直研究的是连续时间一致性(consensus)控制问题，现在想把离散时间控制拾起来。

这篇文章前半部分讲解连续和离散系统的一致性算法，互相做个对比，加深一下印象和理解；后半部分回顾在算法证明中会用到的矩阵理论的基本知识。

下面进入文艺复兴环节，让我们回顾一下最经典的一致性算法和矩阵理论的基本知识吧。

一致性算法

考虑状态 x i ∈ R m x_i\in\mathbb R^m xi​∈Rm，图 G = ( V , E ) \mathcal G=(\mathcal V,\mathcal E) G=(V,E)和单积分器系统
x ˙ i = u i , i ∈ V . \dot x_i=u_i,\quad i\in\mathcal V. x˙i​=ui​,i∈V.

连续时间

首先，给出连续时间一致性算法：
x ˙ i = − ∑ j ∈ N i a i j ( x i − x j ) , i ∈ V , \dot x_i=-\sum_{j\in\mathcal N_i}a_{ij}(x_i-x_j),\quad i\in\mathcal V, x˙i​=−j∈Ni​∑​aij​(xi​−xj​),i∈V,
写成矩阵形式为
x ˙ = − ( L ⊗ I m ) x , \dot x=-(L\otimes I_m)x, x˙=−(L⊗Im​)x,
其中 A = [ a i j ] ∈ R n × n A=[a_{ij}]\in\mathbb R^{n\times n} A=[aij​]∈Rn×n是邻接矩阵(adjacency matrix)，如果 ( j , i ) ∈ E (j,i)\in\mathcal E (j,i)∈E，那么 a i j > 0 a_{ij}>0 aij​>0，否则 a i j = 0 a_{ij}=0 aij​=0； L = [ l i j ] ∈ R n × n L=[l_{ij}]\in\mathbb R^{n\times n} L=[lij​]∈Rn×n是拉普拉斯矩阵(Laplacian matrix)，满足
l i i = ∑ j = 1 , j ≠ i n a i j , l i j = − a i j ,   i ≠ j 。 l_{ii}=\sum_{j=1,j\neq i}^n a_{ij},\qquad l_{ij}=-a_{ij},\,i\neq j。 lii​=j=1,j​=i∑n​aij​,lij​=−aij​,i​=j。

离散时间

然后，给出离散时间一致性算法：
x i , k + 1 = ∑ j ∈ N i d i j x i , k , i ∈ V , x_{i,k+1}=\sum_{j\in\mathcal N_i}d_{ij}x_{i,k},\quad i\in\mathcal V, xi,k+1​=j∈Ni​∑​dij​xi,k​,i∈V,
写成矩阵形式为
x k + 1 = ( D ⊗ I m ) x k , x_{k+1}=(D\otimes I_m)x_{k}, xk+1​=(D⊗Im​)xk​,
其中 k ∈ N k\in N k∈N是离散时间指数(discrete-time index)； D = [ d i j ] ∈ R n × n D=[d_{ij}]\in\mathbb R^{n\times n} D=[dij​]∈Rn×n是行随机矩阵(row-stochastic matrix)，满足 d i i > 0 d_{ii}> 0 dii​>0对所有 i ∈ V i\in\mathcal V i∈V成立，如果 ( j , i ) ∈ E (j,i)\in\mathcal E (j,i)∈E，那么 d i j > 0 d_{ij}>0 dij​>0，否则 d i j = 0 d_{ij}=0 dij​=0。

Vicsek模型¹是离散时间一致性算法的特例，该模型中如果 ( j , i ) ∈ E (j,i)\in\mathcal E (j,i)∈E，那么令 d i j = 1 1 + ∣ N i ∣ d_{ij}=\frac{1}{1+|\mathcal N_i|} dij​=1+∣Ni​∣1​， ∣ N i ∣ |\mathcal N_i| ∣Ni​∣表示智能体 i i i的邻居(neighbor)个数。但是Vicsek模型不一定能保证为双随机矩阵(doubly-stochastic matrix)。已知 L L L的情况下，令 D = e − L D=e^{-L} D=e−L虽然可以得到双随机矩阵，但是无法保证分布式实现。

想要得到满足前面条件的双随机矩阵，一种简单的办法是：如果 ( j , i ) ∈ E (j,i)\in\mathcal E (j,i)∈E，那么令 d i j = 1 / g d_{ij}=1/g dij​=1/g， d i i = 1 − ∑ j ≠ i d i j d_{ii}=1-\sum_{j\neq i} d_{ij} dii​=1−∑j​=i​dij​，其中 g > n g>n g>n。

一致性证明

无论对于连续时间或是离散时间系统，状态 x x x都可以写成关于 t t t或 k k k的函数，即
x ( t ) = ( e − L t ⊗ I m ) x ( 0 ) ， x(t)=(e^{-Lt}\otimes I_m)x(0)， x(t)=(e−Lt⊗Im​)x(0)，
或者
x k = ( D k ⊗ I m ) x 0 。 x_k=(D^k\otimes I_m)x_0。 xk​=(Dk⊗Im​)x0​。
下面需要一致集 S = { x ∈ R n m ∣ x 1 = ⋯ = x n } \mathcal S=\{x\in\mathbb R^{nm}| x_1=\cdots=x_n \} S={x∈Rnm∣x1​=⋯=xn​}是吸引(attractive)的正不变(positive invariant)集，即满足
lim ⁡ t → ∞ e − L t = lim ⁡ k → ∞ D k = 1 n c T ， \lim_{t\to\infty} e^{-Lt}=\lim_{k\to\infty}D^k=1_nc^T， t→∞lim​e−Lt=k→∞lim​Dk=1n​cT，
才有 lim ⁡ t → ∞ x ( t ) = lim ⁡ k → ∞ x k = ( 1 n c T ⊗ I m ) x ( 0 ) \lim_{t\to\infty} x(t)=\lim_{k\to\infty} x_k=(1_nc^T\otimes I_m)x(0) limt→∞​x(t)=limk→∞​xk​=(1n​cT⊗Im​)x(0)。

连续时间

定理1 (Lemma 2.6 ²)：拉普拉斯矩阵 L ∈ R n × n L\in\mathbb R^{n\times n} L∈Rn×n对应的 e − L t , ∀ t ≥ 0 e^{-Lt}, \forall t\geq 0 e−Lt,∀t≥0是主对角元大于0的行随机矩阵。另外， Rank ⁡ ( L ) = n − 1 \operatorname{Rank}(L)=n-1 Rank(L)=n−1当且仅当 L L L有单个0特征根。此外，若 L L L有单个0特征根，且 L T L^T LT关于0特征根的标准化特征向量为 c c c，即
1 n T c = 1 , L T c = 0 , 1_n^Tc = 1,\quad L^Tc = 0, 1nT​c=1,LTc=0,
那么 e − L t → 1 n c T e^{-Lt}\to 1_nc^T e−Lt→1n​cT，当 t → ∞ t\to \infty t→∞。

证明：由于 L L L是方阵，将 − L -L −L特征分解(谱分解)得到 − L = P J P − 1 -L=PJP^{-1} −L=PJP−1，其中 P = [ p 1 , ⋯   , p n ] ∈ R n × n P=[p_1,\cdots,p_n]\in\mathbb R^{n\times n} P=[p1​,⋯,pn​]∈Rn×n， J = diag ⁡ ( 0 , − λ 2 , ⋯   , − λ n ) J=\operatorname{diag}(0,-\lambda_2,\cdots,-\lambda_n) J=diag(0,−λ2​,⋯,−λn​)。不失一般性，我们令 p 1 = 1 n p_1=1_n p1​=1n​对应0特征根，而 λ 2 , ⋯   , λ n \lambda_2,\cdots,\lambda_n λ2​,⋯,λn​都大于0。

由矩阵指数的性质³，易知 e − L t = P e J t P − 1 e^{-Lt}=Pe^{Jt}P^{-1} e−Lt=PeJtP−1。故 e − L t e^{-Lt} e−Lt有特征根1对应特征向量 1 n 1_n 1n​，即 e − L t 1 n = 1 n e^{-Lt}1_n=1_n e−Lt1n​=1n​，因此是行随机矩阵。此外，可以看出 e J t → diag ⁡ ( 1 , 0 , ⋯   , 0 ) e^{Jt}\to \operatorname{diag}(1,0,\cdots,0) eJt→diag(1,0,⋯,0)，当 t → ∞ t\to\infty t→∞，即
P e J t P − 1 → [ 1 n p 2 ⋯ p n ] [ 1 0 ⋯ 0 0 0 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ 0 ] [ c T ν 2 T ⋮ ν n T ] , Pe^{Jt}P^{-1}\to\begin{bmatrix}1_n &p_2&\cdots&p_n\end{bmatrix}\begin{bmatrix}1&0&\cdots &0\\ 0&0&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&0\\ \end{bmatrix}\begin{bmatrix}c^T\\\nu_2^T\\\vdots\\ \nu_n^T \end{bmatrix}, PeJtP−1→[1n​​p2​​⋯​pn​​]⎣⎢⎢⎢⎡​10⋮0​00⋮0​⋯⋯⋱⋯​00⋮0​⎦⎥⎥⎥⎤​⎣⎢⎢⎢⎡​cTν2T​⋮νnT​​⎦⎥⎥⎥⎤​,
当 t → ∞ t\to\infty t→∞。故 e − L t → 1 n c T e^{-Lt}\to 1_nc^T e−Lt→1n​cT，当 t → ∞ t\to\infty t→∞，又因为 e − L t e^{-Lt} e−Lt行随机，即 e − L t 1 n = 1 n ( c T 1 n ) = 1 n e^{-Lt}1_n=1_n(c^T1_n)=1_n e−Lt1n​=1n​(cT1n​)=1n​，故 1 n T c = 1 1_n^Tc=1 1nT​c=1。

引理1 (Lemma C.2)：给定矩阵 A ∈ R n × n A\in\mathbb R^{n\times n} A∈Rn×n和特征根 λ ∈ C \lambda \in\mathbb C λ∈C，假设 x , y x,y x,y满足(i) A x = λ x Ax=\lambda x Ax=λx，(ii) A T y = λ y A^Ty=\lambda y ATy=λy，(iii) x T y = 1 x^Ty =1 xTy=1。如果 ∣ λ ∣ = ρ ( A ) > 0 |\lambda|=\rho(A)>0 ∣λ∣=ρ(A)>0，其中 ρ ( A ) \rho(A) ρ(A)为 A A A的谱半径，且 λ \lambda λ是唯一具有最大模数(maximum modulus)的特征根，那么 lim ⁡ m → ∞ ( λ − 1 A ) m → x y T \lim_{m\to\infty}(\lambda^{-1}A)^m\to xy^T limm→∞​(λ−1A)m→xyT。

A ∈ R n × n A\in\mathbb R^{n\times n} A∈Rn×n是可约矩阵(reducible)，即要么为全0矩阵，要么存在置换矩阵 P ∈ R n × n P\in\mathbb R^{n\times n} P∈Rn×n使得 P T A P P^TAP PTAP为分块上三角阵(block upper triangular form)。 A ∈ R n × n A\in\mathbb R^{n\times n} A∈Rn×n是非负矩阵(nonnegative)，即所有元素都大于等于0。

命题1 (Lemma C.3)：方阵 A ∈ R n × n A\in\mathbb R^{n\times n} A∈Rn×n是不可约的当且仅当与矩阵 A A A对应的有向图 Γ ( A ) \Gamma(A) Γ(A)是强连通的。

引理2 (Lemma C.4)：如果 A ∈ R n × n A\in\mathbb R^{n\times n} A∈Rn×n是非负的不可约(irreducible)矩阵，那么 ρ ( A ) \rho(A) ρ(A)是 A A A的一个特征根，且存在一个非0特征向量 x ≥ 0 x\geq 0 x≥0(即非负)使得 A x = ρ ( A ) x Ax=\rho(A)x Ax=ρ(A)x。

接下来需要证明 c ≥ 0 c\geq 0 c≥0且 c c c是 L L L关于0的左特征向量，即 L T c = 0 L^T c=0 LTc=0。由引理1和引理3可得， c c c是 ( e − L ) T (e^{-L})^T (e−L)T的关于1的特征向量，再由下章的定理1.1， c c c是 L T L^T LT关于0的特征向量。由引理2可知， c ≥ 0 c\geq 0 c≥0。 L L L是不可约矩阵可由强连通性保证，下面的引理3证明 L L L的单个0特征根性质。

一般来说， L L L有至少一个0特征根，而圆盘定理(Gershgorin’s disc theorem)只能确保 L L L的根都位于右半平面或虚轴上，但无法保证0特征根只有一个。事实上，当图 G \mathcal G G不连通时，可能有多个0特征根，且0特征根的个数等于图的连通分量个数。

引理3 (Lemma 2.4)：给定矩阵 A ∈ R n × n A\in\mathbb R^{n\times n} A∈Rn×n，其中 a i i ≤ 0 a_{ii}\leq 0 aii​≤0， a i j ≥ 0 a_{ij}\geq 0 aij​≥0， ∀ i ≠ j \forall i\neq j ∀i​=j，且 ∑ j = 1 n a i j = 0 \sum_{j=1}^n a_{ij}=0 ∑j=1n​aij​=0对任意 i i i成立，那么 A A A有至少一个0特征根和相关的特征向量 1 n 1_n 1n​，其他非0特征根都位于右半开平面。此外， A A A有唯一的0特征根，当且仅当 A A A对应的有向图 Γ ( A ) \Gamma(A) Γ(A)有一个有向生成树(directed spanning tree)。

离散时间

引理4 (Lemma 2.16)：如果一个非负矩阵 A = [ a i j ] ∈ R n A=[a_{ij}]\in\mathbb R^n A=[aij​]∈Rn满足 ∑ j = 1 n d i j = μ > 0 \sum_{j=1}^nd_{ij}=\mu>0 ∑j=1n​dij​=μ>0，那么 μ \mu μ是 A A A关于特征向量 1 n 1_n 1n​的一个特征根，且 ρ ( A ) = μ \rho(A)=\mu ρ(A)=μ，其中 ρ ( ⋅ ) \rho(\cdot) ρ(⋅)表示谱半径。另外，特征根 μ \mu μ的代数重数(algebraic multiplicity)为1，当且仅当 A A A对应的有向图 Γ ( A ) \Gamma(A) Γ(A)有一个有向生成树。此外，如果 d i i > 0 , i = 1 , ⋯   , n d_{ii}>0,i=1,\cdots,n dii​>0,i=1,⋯,n，(i) 那么 ∣ λ ∣ < μ |\lambda|<\mu ∣λ∣<μ对任意 λ ≠ μ \lambda\neq \mu λ​=μ成立，(ii) 如果有向图 Γ ( A ) \Gamma(A) Γ(A)有一个有向生成树，那么 μ \mu μ是唯一具有最大模数的特征根。

证明：矩阵 A A A行和为 μ \mu μ，即 A 1 n = μ 1 n A1_n=\mu 1_n A1n​=μ1n​。再由非负性和圆盘定理， ρ ( A ) ≤ μ \rho(A)\leq \mu ρ(A)≤μ。故 μ \mu μ是 A A A关于特征向量 1 n 1_n 1n​的一个特征根，且 ρ ( A ) = μ \rho(A)=\mu ρ(A)=μ。

(充分性) 若 A A A对应的有向图 Γ ( A ) \Gamma(A) Γ(A)有一个有向生成树，令 B = A − μ I B=A-\mu I B=A−μI，则 B B B满足引理3的条件。 B B B的0根的代数重数为1，自然 A A A的 μ \mu μ根代数重数也为1。

(必要性) (逆否) 若 A A A对应的有向图 Γ ( A ) \Gamma(A) Γ(A)没有向生成树，令 B = A − μ I B=A-\mu I B=A−μI，则 B B B有不止一个0根， A A A的 μ \mu μ根代数重数大于1。

定理2 (Perron-Frobenius theorem)：如果 A ∈ R n × n A\in\mathbb R^{n\times n} A∈Rn×n非负且不可约，那么 (i) ρ ( A ) > 0 \rho(A)>0 ρ(A)>0，(ii) ρ ( A ) \rho(A) ρ(A)是 A A A的一个特征根，(iii) 存在正向量 x x x使得 A x = ρ ( A ) x Ax=\rho(A)x Ax=ρ(A)x，(iv) ρ ( A ) \rho(A) ρ(A)是 A A A的一个代数重数为1(几何重数也为1)的特征根。

一个行随机矩阵 A A A是不可分解且非周期的(indecomposable and aperiodic, SIA)，如果 lim ⁡ k → ∞ A k = 1 n ν T \lim_{k\to \infty}A^k=1_n\nu^T limk→∞​Ak=1n​νT，即极限存在且每一行都相同。

定理3 (Lemma 2.19)：给定行随机矩阵 A ∈ R n × n A\in\mathbb R^{n\times n} A∈Rn×n。如果 A A A有代数重数为1的特征根 λ = 1 \lambda=1 λ=1，且其他特征根满足 ∣ λ ∣ < 1 |\lambda|<1 ∣λ∣<1，那么 A A A是SIA。特别地， lim ⁡ m → ∞ A m → 1 n ν T \lim_{m\to\infty}A^m\to 1_n\nu^T limm→∞​Am→1n​νT，其中 A T ν = ν A^T\nu=\nu ATν=ν且 1 n T ν = 1 1_n^T\nu=1 1nT​ν=1。此外， ν \nu ν的每一个元素非负。

证明：SIA和左特征向量可由引理1直接推出。而 A A A和 A T A^T AT特征根相同(下章的结论2.1)，由引理2可知特征根1对应的特征向量非负。

矩阵理论

主要介绍了特征值、特征向量、特征多项式、代数重数、几何重数以及重要的性质⁴⁵。

特征值和特征向量

这个定理前面有用到，如果0是 L L L的一个特征根，那么 e 0 = 1 e^0=1 e0=1也是 e − L e^{-L} e−L的一个特征根，且它们相应的特征向量都为 1 n 1_n 1n​，反之也一样。

定义 σ ( A ) \sigma (A) σ(A)为矩阵 A A A的特征根集。有几个重要性质：

n n n 阶方阵 A A A是非奇异方阵的充要条件是 A A A可逆，即可逆方阵就是非奇异方阵。以下命题等价：

• 一个矩阵非奇异当且仅当它的行列式不为零。
• 一个矩阵非奇异当且仅当它代表的线性变换是个自同构。
• 一个矩阵半正定当且仅当它的每个特征值大于或等于零。
• 一个矩阵正定当且仅当它的每个特征值都大于零。
• 一个矩阵非奇异当且仅当它的秩为 n n n（满秩）。

证明：如果 λ ∈ σ ( A ) λ∈σ(A) λ∈σ(A)，则存在一个非零向量 x x x，使得 A x = λ x Ax=λx Ax=λx，从而 ( A + μ I ) x = A x + μ x = λ x + μ x = ( λ + μ ) x (A+μI)x=Ax+μx=λx+μx=(λ+μ)x (A+μI)x=Ax+μx=λx+μx=(λ+μ)x。于是 λ + μ ∈ σ ( A + μ I ) λ+μ∈σ(A+μI) λ+μ∈σ(A+μI)。反过来，如果 λ + μ ∈ σ ( A + μ I ) λ+μ∈σ(A+μI) λ+μ∈σ(A+μI)，则存在非零向量 y y y，使得 A y + μ y = ( A + μ I ) y = ( λ + μ ) y = λ y + μ y Ay+μy=(A+μI)y=(λ+μ)y=λy+μy Ay+μy=(A+μI)y=(λ+μ)y=λy+μy。于是 A y = λ y Ay=λy Ay=λy, 从而 λ ∈ σ ( A ) λ∈σ(A) λ∈σ(A)。

特征多项式

证明：

1. 多项式次数最高的两项和常数项已经给出，而其他求和项包含非对角因子 − a i j -a_{ij} −aij​，故次数不会大于 n − 2 n-2 n−2，因为 t − a i j t-a_{ij} t−aij​和 t − a j j t-a_{jj} t−ajj​不是因子。
2. p A ( λ ) = 0 ⇔ det ⁡ ( λ I − A ) = 0 ⇔ ( λ I − A ) x = 0 , x ≠ 0 ⇔ λ ∈ σ ( A ) p_A(λ)=0⇔\operatorname{det}(λI−A)=0⇔(λI−A)x=0,x≠0⇔λ∈σ(A) pA​(λ)=0⇔det(λI−A)=0⇔(λI−A)x=0,x​=0⇔λ∈σ(A)
3. 次数为 n ⩾ 1 n⩾1 n⩾1的多项式至多有 n n n个不同零点。

p A ( t ) p_A(t) pA​(t)的零点之和是 A A A的迹 tr ⁡ ( A ) \operatorname{tr}(A) tr(A)，而零点之积则是 A A A的行列式 det ⁡ ( A ) \operatorname{det}(A) det(A)。

代数重数

λ λ λ的代数重数是特征方程里面有几个根是 λ λ λ。

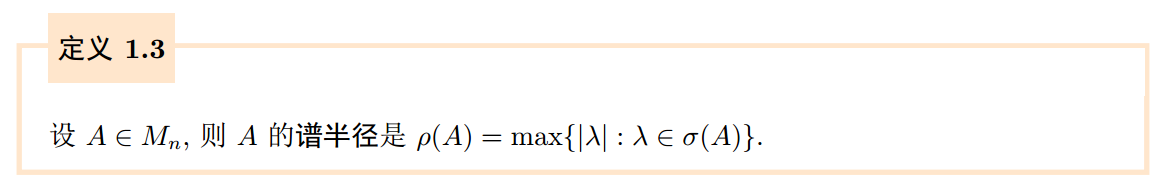
矩阵的谱半径(spectral radius)是模最大特征根对应的模数。

上述定理表明，一个奇异的复矩阵总可以稍加平移使之成为非奇异的。

几何重数

证明：由于 det ⁡ ( t I − A T ) = det ⁡ ( t I − A ) T = det ⁡ ( t I − A ) \operatorname{det}(tI−A^T)=\operatorname{det}(tI−A)^T=\operatorname{det}(tI−A) det(tI−AT)=det(tI−A)T=det(tI−A), 我们有 p A T ( t ) = p A ( t ) p_{A^T}(t)=p_A(t) pAT​(t)=pA​(t), 所以有 p A T ( λ ) = 0 p_A^T(λ)=0 pAT​(λ)=0 当且仅当 p A ( λ ) = 0 p_A(λ)=0 pA​(λ)=0。 类似地， det ⁡ ( t ˉ I − A ∗ ) = det ⁡ [ ( t I − A ) ∗ ] = det ⁡ ( t I − A ) ‾ \operatorname{det}(\bar tI−A^∗)=\operatorname{det}[(tI−A)^∗]=\overline{\operatorname{det}(tI−A)} det(tˉI−A∗)=det[(tI−A)∗]=det(tI−A)​, 所以 p A ∗ ( t ˉ ) = p A ( t ) ‾ p_{A^∗}(\bar t)=\overline {p_A(t)} pA∗​(tˉ)=pA​(t)​, 又 p A ∗ ( λ ˉ ) = 0 p_A^∗(\bar λ)=0 pA∗​(λˉ)=0当且仅当 p A ( λ ) = 0 p_A(λ)=0 pA​(λ)=0。

如果 x , y ∈ C n x,y∈\mathbb C^n x,y∈Cn两者都是 A ∈ M n A∈M^n A∈Mn的与特征值 λ λ λ相伴的特征向量，那么 x x x与 y y y的任何非零的线性组合也是它的与 λ \lambda λ相伴的特征向量 。实际上，与一个给定的 λ ∈ σ ( A ) λ∈σ(A) λ∈σ(A)相伴的所有特征向量组成的集合与零向量合起来作成 C n \mathbb C^n Cn的一个子空间，该子空间就是 A − λ I A−λI A−λI的零空间，就是齐次线性方程组 ( A − λ I ) x = 0 (A−λI)x=0 (A−λI)x=0的解集，由秩的关系知其维数是 n − rank ⁡ ( A − λ I ) n−\operatorname{rank}(A−λI) n−rank(A−λI)。该空间有个名字就是特征空间，下面给出特征空间的完整定义：

介绍完特征空间，就可以定义几何重数了，特征空间的维数即为几何重数。

可以证明特征值的几何重数小于或者等于它的代数重数的。

即，几何重数 = n − rank ⁡ ( A − λ I ) ≤ k = =n-\operatorname{rank}(A-\lambda I)\leq k= =n−rank(A−λI)≤k=代数重数。

一个矩阵可对角化，当且仅当它是无亏的；它有完全不同的特征值，当且仅当它是无损的且是无亏的。考虑以下矩阵的特征值 λ = 1 λ=1 λ=1, 矩阵 [ 1 0 0 2 ] \begin{bmatrix}1&0\\ 0&2\end{bmatrix} [10​02​]，代数重数等于它的几何重数且都是 1, 它是无亏的，单位矩阵 I 2 I_2 I2​是无亏的且是有损的，矩阵 [ 1 1 0 1 ] \begin{bmatrix}1&1\\ 0&1\end{bmatrix} [10​11​]，几何重数是1, 代数重数是2，它是有亏的且是无损的。

尽管 A A A与 A T A^T AT有相同的特征值，它们与给定特征值相伴的特征空间有可能是不同的。比如，矩阵 A = [ 2 3 0 4 ] A=\begin{bmatrix}2&3\\ 0&4\end{bmatrix} A=[20​34​]，那么 A A A的与特征值2相伴的（一维）特征空间是由 [ 1 0 ] \begin{bmatrix}1\\ 0\end{bmatrix} [10​]生成的，而 A T A^T AT的与特征值2相伴的特征空间是由 [ 1 0 0 − 3 / 2 ] \begin{bmatrix}1&0\\ 0&-3/2\end{bmatrix} [10​0−3/2​]生成的。

总结

• λ λ λ的代数重数是特征方程里面有几个根是 λ λ λ。
• λ λ λ的几何重数是线性空间 A x = λ x Ax=λx Ax=λx的维数。
• 代数重数大于等于几何重数，代数重数如果大于几何重数，那么原因在于这个矩阵的Jordan标准型里面有维数大于1的Jordan块。
• 强连通 ⇔ \Leftrightarrow ⇔有向生成树 ⇔ \Leftrightarrow ⇔不可约 ⇔ \Leftrightarrow ⇔最大模数特征根代数重数为1 ⇔ \Leftrightarrow ⇔相应特征向量非负
• 如果是行随机，则上面条件 ⇔ \Leftrightarrow ⇔SIA ⇔ \Leftrightarrow ⇔极限为 1 n ν T 1_n\nu^T 1n​νT，其中 ν \nu ν为左特征向量

---

1. Vicsek, T., Czirók, A., Ben-Jacob, E., Cohen, I., Shochet, O. (1995). Novel type of phase transition in a system of self-driven particles. Physical review letters, 75(6), 1226. ↩︎

2. Ren, W., & Beard, R. W. (2008). Distributed consensus in multi-vehicle cooperative control . London: Springer London. ↩︎

3. 矩阵指数. (2020, September 15). Retrieved from 维基百科, 自由的百科全书: https://zh.wikipedia.org/w/index.php?title=%E7%9F%A9%E9%98%B5%E6%8C%87%E6%95%B0&oldid=61692808 ↩︎

4. 特征值和特征向量. 小鱼吻水. https://www.cnblogs.com/zhoukui/p/7672972.html ↩︎

5. 特征多项式、代数重数与几何重数. 小鱼吻水. https://www.cnblogs.com/zhoukui/p/7685318.html ↩︎