程序员经验分享-hwhale

如何理解矩阵相乘的几何意义或现实意义？

2023-05-16
作者：deng will
链接：https://www.zhihu.com/question/28623194/answer/135658852
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

这个问题我也思考了许久，如何从高中的知识过度到大学的线代知识，偶然间看到一篇文章再结合MIT的线代和国内的西工大的矩阵论的一小撮知识，终于把这个问题可以详细的写出来了，达到知其所以然。（欢迎大家指正错误）
我们先来看一个高中就学过的向量运算：内积。A=（x1，y1），B=（x2，y2），如下图所示
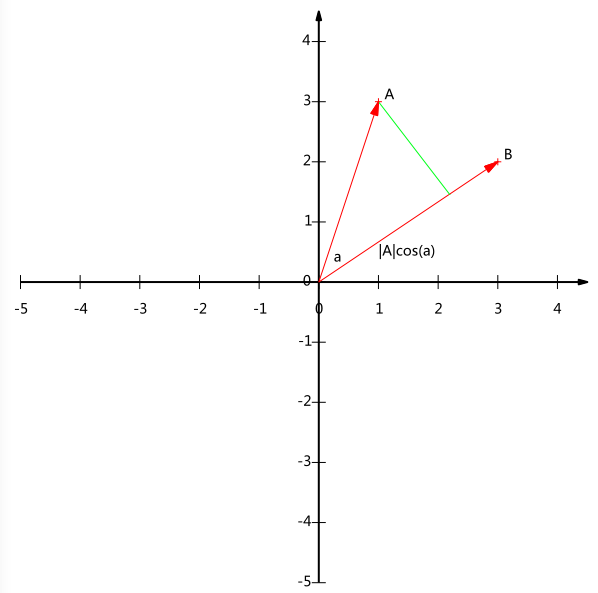
<img src="https://pic4.zhimg.com/50/8d64151ceed0eed4d4708d8d9e6374dc_hd.jpg" data-rawwidth="598" data-rawheight="593" class="origin_image zh-lightbox-thumb" width="598" data-original="https://pic4.zhimg.com/8d64151ceed0eed4d4708d8d9e6374dc_r.jpg"> 好，我们从A点向B所在直线引一条垂线，我们知道垂线与B的交点叫做A在B上的投影，不过我们如果将内积表示为另一种我们熟悉的形式： A*B=|A||B||cos(a)|,我们可以看到A与B的内积等于A到B的投影长度乘以B的模，再进一步，令|B|=1，那么就变成了 A*B=|A||cosa|。
我们继续在二维空间讨论向量，一个向量（3,2）本身是不能精确表示一个向量的，实际上隐含了再X轴投影为3而Y轴的投影为2，更正式的，向量（x,y）实际上可以表示为<img src="https://pic3.zhimg.com/50/4533331b5b4b5ea98c90f2abed81d470_hd.jpg" data-rawwidth="598" data-rawheight="594" class="origin_image zh-lightbox-thumb" width="598" data-original="https://pic3.zhimg.com/4533331b5b4b5ea98c90f2abed81d470_r.jpg"> X*\left( \begin{array}{ccc}1 \\0 \end{array}\right) +X*\left( \begin{array}{ccc}0 \\1 \end{array}\right)，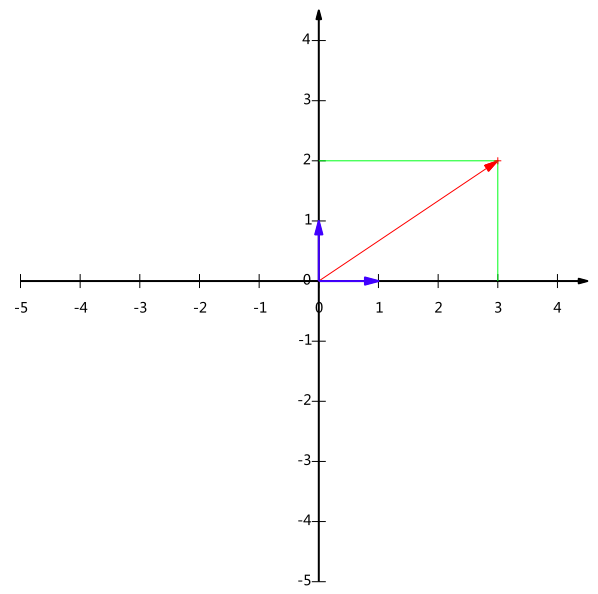此处（1,0）和（0,1）叫做二维空间的一组基。

我们之所以默认选择(1,0)和(0,1)为基，当然是比较方便，因为它们分别是x和y轴正方向上的单位向量，因此就使得二维平面上点坐标和向量一一对应，非常方便。但实际上任何两个线性无关的二维向量都可以成为一组基，所谓线性无关在二维平面内可以直观认为是两个不在一条直线上的向量。

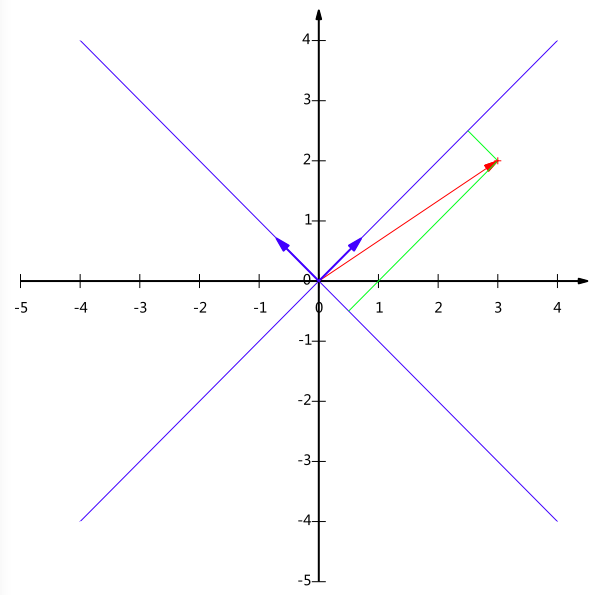
例如，(1,1)和(-1,1)也可以成为一组基。一般来说，我们希望基的模是1，因为从内积的意义可以看到，如果基的模是1，那么就可以方便的用向量点乘基而直接获得其在新基上的坐标了！实际上，对应任何一个向量我们总可以找到其同方向上模为1的向量，只要让两个分量分别除以模就好了。例如，上面的基可以变为下图所示，(\frac{1}{\sqrt{2} }, \frac{1}{\sqrt{2} })，(-\frac{1}{\sqrt{2} }, \frac{1}{\sqrt{2} })（注：基都为列向量，这是遵循MIT教授的课上的建议，但是为了表示方便，我混用了。）现在我们想获得（3,2）在新基上的坐标，即在两个方向上的投影矢量值。

根据程云鹏的矩阵论11页上的定义：设x1，x2，...，xn是Vn的旧基，y1，y2，...，yn为其新基，则由基的定义可以写为（y1，y2，...，yn）=（x1，x2，...，xn）C（此处y和x均为列向量），

<img src="https://pic3.zhimg.com/50/v2-792e7958dd784ec8a91abb6344342a9c_hd.jpg" data-rawwidth="639" data-rawheight="362" class="origin_image zh-lightbox-thumb" width="639" data-original="https://pic3.zhimg.com/v2-792e7958dd784ec8a91abb6344342a9c_r.jpg">


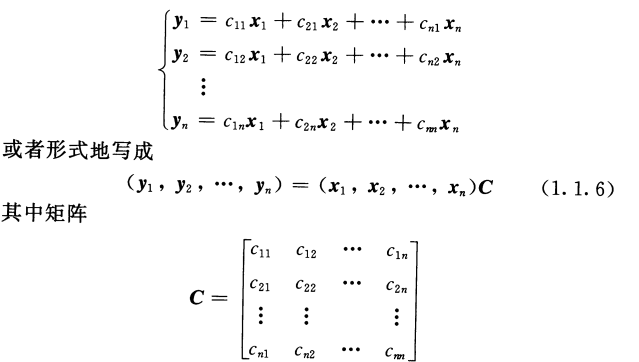
其中C称之为过渡矩阵

所以我们有Y=X*C,其中Y为\left( \begin{array}{ccc}\frac{1}{\sqrt{2} } &-\frac{1}{\sqrt{2} } \\\frac{1}{\sqrt{2} }&\frac{1}{\sqrt{2} }\end{array}\right),X为\left( \begin{array}{ccc}1&0 \\0&1 \end{array}\right),可得C为\left( \begin{array}{ccc}\frac{1}{\sqrt{2} } &-\frac{1}{\sqrt{2} } \\\frac{1}{\sqrt{2} }&\frac{1}{\sqrt{2} }\end{array}\right)，

<img src="https://pic4.zhimg.com/50/ff47d66fa67d12918e4e83678fa6b78d_hd.jpg" data-rawwidth="598" data-rawheight="595" class="origin_image zh-lightbox-thumb" width="598" data-original="https://pic4.zhimg.com/ff47d66fa67d12918e4e83678fa6b78d_r.jpg">

那么根据程云鹏的矩阵论书中，坐标在新基中的表示为C^{-1}*\left( \begin{array}{ccc}3 \\2 \end{array}\right)=\left( \begin{array}{ccc}\frac{5}{\sqrt{2} } \\-\frac{1}{\sqrt{2} } \end{array}\right)

我们可以看到C明显为正交矩阵，正交矩阵的性质为

正交矩阵的逆等于其转置,所以本来C的第一列为基，求逆矩阵之后变成C的第一行为基。
所以推导出下面这个式子。
一般的，如果我们有M个N维向量，想将其变换为由R个N维向量表示的新空间中，那么首先将R个基按行组成矩阵A，然后将向量按列组成矩阵B，那么两矩阵的乘积AB就是变换结果，其中AB的第m列为A中第m列变换后的结果。
数学表示为：<img src="https://pic1.zhimg.com/50/v2-aca27e96cfa51d1b0fcb265d9918ad83_hd.jpg" data-rawwidth="771" data-rawheight="179" class="origin_image zh-lightbox-thumb" width="771" data-original="https://pic1.zhimg.com/v2-aca27e96cfa51d1b0fcb265d9918ad83_r.jpg"> 特别要注意的是，这里R可以小于N，而R决定了变换后数据的维数。也就是说，我们可以将一N维数据变换到更低维度的空间中去，变换后的维度取决于基的数量。因此这种矩阵相乘的表示也可以表示降维变换。
最后，上述分析同时给矩阵相乘找到了一种物理解释： 两个矩阵相乘的意义是将右边矩阵中的每一列列向量变换到左边矩阵中每一行行向量为基所表示的空间中去。更抽象的说，一个矩阵可以表示一种线性变换。很多同学在学线性代数时对矩阵相乘的方法感到奇怪，但是如果明白了矩阵相乘的物理意义，其合理性就一目了然了
参考文献：
1. PCA数学原理
2.矩阵论--程云鹏
3.Introduction to Linear Algebra--GILBERT STRANG
本文内容由网友自发贡献，版权归原作者所有，本站不承担相应法律责任。如您发现有涉嫌抄袭侵权的内容，请联系:hwhale#tublm.com(使用前将#替换为@)

如何理解矩阵相乘的几何意义或现实意义？ 的相关文章

  • Unix环境高级编程读书笔记之二——文件I/O

  • VNC连接ubuntu10.04出现白屏问题解决

    使用vnc登陆界面如下 解决办法 xff1a 将 vnc xstartup文件中最后一行x window manager amp 使用 注释掉 xff0c 然后添加一行gnone session amp 然后退出所有的XWINDOWS xf

  • vnc viewer上的分辨率

    问题 xff1a 用vnc远程连接时的系统屏幕即便最大化之后 xff0c 屏幕也只是中间的一小块屏幕 xff0c 并没有跟着vnc的最大化而最大化 解决办法 xff1a 连接窗口时点选option xff0c 或者VNC窗口标题栏右键 gt

  • 在Linux中Oracle安装成功后，首次启动使用时，会出现的一些问题总结和解决办法

    注意 xff1a oracle安装不能用root用户安装 xff0c 必须新建用户安装 1 sqlplus 命令不识别问题 xff08 bash xff1a sqlplus command not found xff09 当你首次安装ora

  • 树莓派安装系统和系统备份还原

    最近有使用到树莓派做一些项目 xff0c 下面整理了下树莓派烧录系统到系统镜像备份还原的一些方法 在操作中尝试了windows和ubuntu两个系统下的烧录方式 1 树莓派官网下载Raspberry Pi Imager 登录树莓派官网 找到

  • Gazebo仿真环境中odom和baselink关联一起

    在Gazebo仿真环境中使用slam gmapping采图时发现 xff0c 没有odom数据 xff0c topic map没有数据 通过tf tree发现 odom没有和base link建立关联 日志上可以看到odom完全没有 这需要

  • 相机的变焦，对焦和景深的理解和照相機的成像原理

    首先认识焦距 xff1a 是指平行光线经透镜折射或曲面镜反射后的会聚点 xff0c 点到镜片中心的距离就是f焦距 相机成像时最清晰的位置就是感光阵列位于焦点处 焦距的作用 xff1a 焦距的大小决定着相机视野的范围大小 xff0c 一般焦距

  • 内参、外参、畸变参数三种参数与相机的标定方法与相机坐标系的理解

    有国才有家 xff0c 支持国产 xff0c 生活中点滴做起 xff0c 买手机就买华为 xff0c 这是我们国家IT界的脊梁 xff01 xff01 xff01 1 相机参数是三种不同的参数 相机的内参数是六个分别为 xff1a 1 dx

  • 基于ubuntu16.04配置VNC远程连接

    VNC官网下载https www realvnc com en connect download vnc linux 下载后的文件是VNC Server 6 3 1 Linux x86 deb xff0c 执行命令 xff1a sudo d

  • 关于Ubuntu与Debian的关系，了解！

    饮水思源 xff1a Ubuntu用户应关注Debian 当今最热门的桌面Linux非Ubuntu莫属 xff0c 它已经拥有数量众多的爱好者 xff0c 已经成为PC用户的主流操作系统之一 尽管Ubuntu相对还比较年 轻 xff0c 但

  • 最优化问题及其分类

    优化技术是一种以数学为基础 xff0c 用于求解各种工程问题优化解的应用技术 归纳而言 xff0c 最优化问题分为函数优化问题和组合优化问题两大类 xff0c 其中函数优化的对象是一定区间的连续变量 xff0c 而组合优化的对象则是解空间中

  • 50个有趣的休闲网站 (外国)

    有选择的余地是件好事 xff0c 但是如果选择太多了也让人烦恼 我们在网络上进行了搜索 xff0c 挑出了50个最有用而有趣的网站 今天互联网已经是很大的生意 无论你是想要购买一辆汽车 出售家庭产品 做生意或者收集难以找到的信息 xff0c

  • 一个不错的技术面试官是怎么样的？

    一个不错的技术面试官是怎么样的 xff1f 转载自 xff1a http t cn AiWwBM2b 作者 Jartto 作为技术面试官 xff0c 面试过程很少考虑候选人的感受 上来就是问 xff0c 不合适就送走 虽然技术环节我很专业

  • SVN update 返回值的含义

    本文来自网络 当你从代码库里面更新自己本地的工作拷贝的时候 xff0c update返回的值意思如下 xff1a u foo 文件foo更新了 xff08 从服务器收到修改 xff09 A foo 文件或目录foo被添加到工作拷贝 D fo

  • Linux DRM Graphic 显示简单介绍

    好久没有写过博客了 xff0c 工作之后平时都没有总结 xff0c 感觉像做了学到很多东西 xff0c 但是又感觉什么都没有学到 xff0c 似懂非懂 xff08 真尼玛纠结 xff09 突然别人说的一句话 xff0c 学东西不仅仅是自己学

  • Linux DRM KMS 驱动简介

    Whoops xff0c 上次写完 Linux DRM Graphic 显示简单介绍 博文后 xff0c 心情还是蛮愉悦的 xff0c 来来 xff0c 这次在说说具体的显卡驱动 1 DRM 框架分解 DRM 框架提供了一系列的 IOCTL

  • Vim 自动补全插件 YouCompleteMe 安装与配置

    本文系转载文章 xff0c 原文链接 http howiefh github io 2015 05 22 vim install youcompleteme plugin Contents 1 概述 2 安装 2 1 完全安装 2 2 Ub

  • Linux 中的各种栈：进程栈 线程栈 内核栈 中断栈

    转载请注明出处 xff1a http kyang cc 栈是什么 xff1f 栈有什么作用 xff1f 首先 xff0c 栈 stack 是一种串列形式的 数据结构 这种数据结构的特点是 后入先出 LIFO Last In First Ou

  • SD-WAN 到底是什么？

    转载请注明出处 xff1a http kyang cc In a nutshell SD WAN Virtualizes the networkEnables a secure overlaySimplifies services deli

  • SDN, SD-WAN, NFV, VNF: What Is All This?

    本文转载至 xff1a http www velocloud com sd wan blog sdn sd wan nfv vnf Inscrutable alphabet soup Even the fully expanded term

随机推荐

  • Top-down Design简介

    自顶向下 xff0c 逐步求精的方法 在英文中称作Top down Design xff0c 是一种计算机编程使用的算法思想 xff0c 顾名思义 xff0c 这种方法的思想就是对现在遇到的复杂或者抽象化的问题 xff0c 进行纵向深入分解

  • The Advantages of SD‐WAN over Traditional WAN

    转载请注明出处 xff1a http kyang cc An SD WAN has several advantages over a traditional WAN 重点内容 Simplified WAN Rapid deployment

  • 玩转 SSL 证书

    Introduction Openssl 是一个很牛逼的工具 xff0c 基本能搞定 PKI amp HTTPS 证书相关的事情 这篇博文归类了一堆常用的命令 xff0c 全部都是关于 key amp csr amp crt 本文分成两部分

  • linux简易书单

    1 Linux程序设计 xff08 第4版 xff09 万千读者推荐的Linux经典入门书 程序设计实战型图书 xff0c 以简单易懂 内容全面和示例丰富而受到广泛好评 如果你没有Linux基础 xff0c 可以先读这本 话说回来 xff0

  • 数字图像处理的技术方法和应用

    所谓数字图像处理 xff0c 是指将图像信号转换成数字信号并利用计算机对其进行处理的过程 20 世纪 50 年代 xff0c 电子计算机已经发展到一定水平 xff0c 人们开始利用计算机来处理图形和图像信息 xff0c 这便是早期的图像处理

  • hadoop安装完后打开网页http://localhost:50070/ 没反应

    在hadoop安装完后 xff0c 依次执行hadoop namenode format xff0c start dfs sh xff0c start yarn sh 之后 打开浏览器 输入 http localhost 50070 无反应

  • 关于CSDN代码段的背景颜色修改

    当我第一次去在CSDN中写代码时会发现自己的是用的 代码段 是如图下所示这种黑色的背景 那么自己想要去修改因该如何设置 1 鼠标悬停到头像上 2 点击内容管理标签 3 点击博客设置 4 在代码片样式中选择自己喜欢的样式就可以了

  • 利用VSPD、串口调试助手、Keil做串口调试

    下面详细介绍下如何用虚拟串口调试串口发送接收程序 需要用到三个软件 xff1a KEIL VSPD XP5 xff08 virtual serial ports driver xp5 1虚拟串口软件 xff09 串口调试助手 xff08 个

  • 基于机器学习的雷达信号分选和目标识别（论文阅读学习记录—持续记录）

    机器学习在雷达信号分选技术上的应用包括信号分离 确定脉冲参数 形成单部雷达脉冲序列 xff0c 然后针对雷达目标识别进行分类并划分威胁程度等 在一维距离像识别过程中包括去噪和雷达目标型号识别 该论文 xff08 学习内容 xff09 重点研

  • CMake Error: The following variables...set to NOTFOUND

    今天在编译开源OpenVslam时 xff0c 在最后阶段出现如下问题 说是DBOW2的库招不到 查看了dbow2都是正常安装的 xff0c 但是就是出问题 然后我就找到了对应的cmakelist txt文件 xff0c 将LIBS地址打印

  • PCL库调试过程中，显示当前不会命中断点，还没有为该文档加载任何符合

    最近在读PCL库中NDT源码 xff0c 搞了一个vs2019的工程将NDT部分跑了起来 xff0c 想通过打断点的方式进入源码中一步步走读代码 但是有些部分的源码可以通过断点的方式进 hpp文件 xff0c 有些确不能 比如kdtree

  • 相机矩阵（camera matrix）

    本博文主要介绍camera的参数矩阵 目录 相机小孔模型 相机矩阵 xff08 内参 xff09 相机矩阵 xff08 Intrinsic matrix xff09 图像坐标系 相机的外参矩阵 xff08 extrinsic matrix

  • Pytorch模型转ONNX

    参考https blog csdn net qq 37546267 article details 106767640 利用下面代码将pth模型转换为onnx import torch from torch autograd import

  • File already exists in database google/protobuf/descriptor.proto

    以加载静态库的方式加载protobuf库时出现如下问题 xff1a libprotobuf ERROR google protobuf descriptor database cc 57 File already exists in dat

  • assign()测试

    assign 应该属于赋值 std deque lt int gt di 1 2 3 4 5 std cout lt lt 34 at first 34 lt lt std endl std cout lt lt 34 di 61 34 f

  • 解析力评测（1） MTF和SFR

    成像系统的解析力一直是摄像头最关键的指标之一 所有用户拿到一张照片的时候首先看到的是照片清楚不清楚 xff0c 图像的清楚说得就是解析力 但是如何评价一个成像系统的解析力也是大家一直在探讨的问题 目前主流的办法主要有三种TV line检测

  • MTF的倾斜边缘计算方法

    简介 光学系统性能的衡量方法有很多 xff0c 常见的有点扩散函数法 瑞利判断法 点列图法 光学传递函数 MTF 法等 xff0c 其中MTF法在光学系统和镜头加工制造中使用最为广泛 MTF曲线真实的反映了成像系统将物方信息传递到像方的能力

  • 机器人学中旋转矩阵与欧拉角之间互换公式及程序

    弧度 角度 define PAI 3 141592653589793 define RADIAN PAI 180 0 弧度 61 角度 180 define ANGLE 180 0 PAI 角度 61 弧度 180 2 旋转矩阵转换为欧拉角

  • opencv 读取图片并提取Mat中data数据

    uchar pImageData 61 uchar malloc width height 3 sizeof uchar Mat MyImage 61 imread file name IMREAD COLOR if MyImage dat

  • 如何理解矩阵相乘的几何意义或现实意义？

    作者 xff1a deng will 链接 xff1a https www zhihu com question 28623194 answer 135658852 来源 xff1a 知乎 著作权归作者所有 商业转载请联系作者获得授权 xf

热门标签