最近几天在整理高斯过程回归(Gaussian Process Regression, GPR)部分的知识，虽然还有很多问题没有搞懂，但是有一点进展还是决定总结下来，防止遗忘。
在整理之前，先列出我参考的几个资料吧，一方面方便大家参考，另一方面也防止自己以后找不到了。
GPR部分一共有两种理解角度：权重空间(Weight-Space View)与函数空间(Function-Space View)。这里先说Weight-Space View。先描述一下问题，现有一个未知的模型，可以确性的信息是：这个模型是线性的，并且输出端还带有零均值且服从高斯分布的噪声。通过数据采集得到了一些输入-输出数据，现在需要做的是利用GPR部分的原理，求出原线性模型中的未知参数的概率分布，并且这个概率分布要使用高斯分布去描述。下边将用公式表示以上文字：
现有N组可以被视为独立同分布的训练数据：。其中，
为列向量，
为一实数。现该线性模型可以被如下表示：
其中，为列向量，
服从零均值高斯分布。为表示方便，将输入数据和输出数据分别用一个符号表示：
贝叶斯估计就是求出在已知训练数据时，参数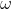的概率分布。即“最大后验概率”。不严格地，也可以理解为中学阶段的“条件概率”。这里需要引入一个概念：贝叶斯学派与频率学派。
经典的频率学派认为：一个随机事件发生的概率是固定的，属于这个事件本身的属性，并不会随着采集样本的变化而发生改变。因此，频率学派的“估计”指的是，在已知概率分布参数的条件下，去计算我们采集的样本是如何分布。是一种“这个参数的数值就是不变的，我们看看这个随机事件的样本该如何分布吧！”的感觉。
但是贝叶学派正好与之相反，贝叶斯学派认为随机事件发生的概率是一个非常主观的数值，并且这个数值还会随着采集样本的不同而发生改变。因此，贝叶斯学派的“估计”指的是，在样本已知的条件下，反推这个随机事件的参数是如何分布的。有一种“随着认知的深入，我们对事物的评价就更加准确啦！”的感觉。
言归正传，求参数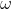的后验概率就是在求表达式
的表达形式。这里简单推导一下：
利用两个等式最右端彼此相等可以得到：
这里个人理解是：贝叶斯理论认为采样数据是客观存在的，并不会因为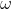如何如何就发生改变，因此
。得到这个式子之后，就可以用本科和硕士研究生阶段学习的概率论和引用数理统计的知识了。其中
被称为似然函数(likelihood)，
被称为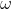
的先验概率(prior)，
被称为边缘化似然函数(marginal likelihood)。上式的分布是一个与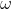
无关的常数，因此，后验概率也可以如下表示：
似然函数可以表示为n个独立同分布的乘积形式：。根据文章前边的线性模型的表达式和中学阶段学过的正态分布的性质可以知道，每一个输出样本的概率分布均为：
。因此，可以推导出似然函数的表达式：
其中，为一个数量。A的化简如下：
因此，似然函数就可以被表达成如下形式：
对比多元高斯分布的标准公式，我们可以看出这个服从高斯分布的似然函数可以被如下表示：
根据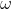的后验概率正比于似然函数和先验概率的乘积这一事实。在这里我们假设
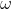的先验分布已知：
因此，将两个表达式代入，可以得到：
根据高斯分布的特征参数可以直接从指数项中提炼出来，而不需要看前边增益系数的特点，我们可以对上式进行化简：
乍一看这个公式没有规律可言。我们先整理一下标准的多元高斯分布的概率密度表达式：
从这个公式，我们可以看到。多元高斯分布的概率密度表达式的指数项中有二次项、一次项和常数项。我们只需要将相同项的系数对应起来即可。通过观察，可以发现：
进一步地，可以求出参数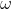的后验概率分布为(
为对称矩阵)：
至此，参数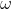的后验概率求解完成。利用得到的参数分布去估计在测试点x*时的y值，只需要将模型代入即可：
本文只是GPR部分的推导，并不涉及GPR在具体问题中应该如何设计程序和迭代。个人感觉还是理解不够深入，如果哪里有错误还烦请各位指导纠正！！
