【高数】Abel定理，幂级数的和收敛半径，不同幂级数收敛半径的比较，缺项幂级数的解法

2023-11-14

一、收敛区间及收敛点

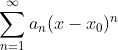$\sum_{n=1}^{\infty }a_{n}(x-x_{0})^{n}$ ，现对该形式的幂级数进行如下讨论。

1. 幂级数的收敛区间，对称中心是x0，收敛半径是R。

2. 经有限次的逐项求导或积分，不改变收敛半径R和收敛去间（x0-R, x0+R），但收敛域可能改变。

即收敛区间端点处的敛散性可能会改变。

3. 由Abel定理，若x1处收敛（x1≠x0），那么满足 |x-x0|<|x1-x0| 的x值，均绝对收敛。但不知 |x-x0|>|x1-x0| 时的敛散性。

若x2处发散（x1≠x0），那么对满足 |x-x0|>|x2-x0| 的任何x值，均发散。

可简单理解为，已知一个收敛点，那么其他离收敛区间的中心更近的，就绝对收敛。比发散点更远的，就发散。

这部分是不是很像正项级数的比较审敛法，是的！事实上，当我们代入两个确定的x值时，比如x1和x3，而x3更近。此时，二者都是常数项函数，我们取绝对值，研究其是否绝对收敛。那么自然就有x1的级数>x3代入后的，又因为“大级数收敛则小级数收敛”，所以这个必然就收敛。

突然发现，幂级数和正项级数存在联系，这为我们求幂级数的收敛区间提供了线索，见标题二。

《2018考研数学中幂级数的收敛半径、收敛区间与收敛域》：http://kaoyan.xdf.cn/201706/10687275.html

文章给出了 x^n 及 (x-x0)^n 两种形式幂级数的Abel定理，以及例题。

4. 由3推出，当某点处条件收敛时，该点必然为区间端点。反之未必！

因为收敛区间的端点，是条件收敛或发散的。

二、收敛半径的变化

1. 幂级数的和

《关于2个幂级数和的收敛半径的说明》：https://www.docin.com/p-1179115014.html

两个幂级数相加减，收敛半径 ≥ 原来的收敛半径的较小值。

2. 幂级数之间的比较：如级数a的通项<级数b的通项，而b是收敛的，那么a的收敛半径 Ra ≥ Rb。

可简单理解，选取相同的x0值代入级数，使b收敛的值必能使a收敛，所以a的半径至少要包括b。可记忆为，小级数收敛的速度更快，较远的点都能保证收敛，其收敛半径反而大。

三、借助正项级数敛散性求幂级数收敛区间

即可以把 x 当作参数，使用正项级数的各种判别法，最终求出 x 的取值范围。见下面的例子。

四、缺项幂级数的解法

思路一：代入通项时，注意脚标，an的n不表示代入了n，而表示和x的次方对应的那个通项！实际上是在脑海中完成了变量替换，容易糊涂，不推荐。

思路二：变量替换。

思路三：把 x 当成参数，按正项级数做。

《缺项幂级数收敛域的求法》：https://wenku.baidu.com/view/547216fa700abb68a982fb73.html

讨论了为什么不可以对缺项幂级数直接求相邻系数比值。

《奇数项和偶数项幂级数的收敛半径求法》：https://zhuanlan.zhihu.com/p/32579738

认为：偶数项（1）求出收敛半径后，分析x^2与x的关系，即收敛半径应开根号（2）当成数项级数

奇数项（1）提出一个x或1/x，不改变收敛半径，转为偶数项研究（2）当成数项级数

五、小结

1. 幂级数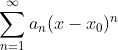 $\sum_{n=1}^{\infty }a_{n}(x-x_{0})^{n}$ 的收敛区间，对称中心是x0，收敛半径是R。

2. 经有限次的逐项求导或积分，不改变收敛半径R和收敛去间（x0-R, x0+R），但收敛域可能改变。

3. 由Abel定理，若x1处收敛（x1≠x0），那么满足 |x-x0|<|x1-x0| 的x值，均绝对收敛。但不知 |x-x0|>|x1-x0| 时的敛散性。

若x2处发散（x1≠x0），那么对满足 |x-x0|>|x2-x0| 的任何x值，均发散。

4. 当某点处条件收敛时，该点必然为区间端点。反之未必！

5. 缺项幂级数的解法：

思路一：代入通项时，注意脚标。
思路二：变量替换。
思路三：把 x 当成参数，按正项级数做。

本文内容由网友自发贡献，版权归原作者所有，本站不承担相应法律责任。如您发现有涉嫌抄袭侵权的内容，请联系:hwhale#tublm.com(使用前将#替换为@)

高等数学